
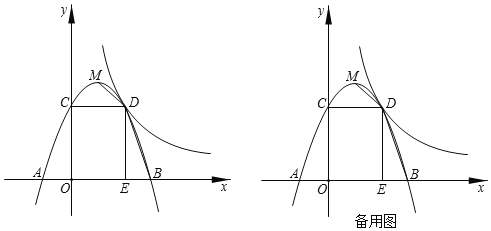
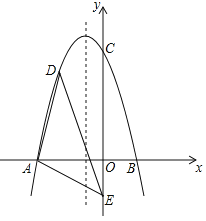
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C,过点C作CD⊥y轴交抛物线于另一点D,作DE⊥x轴,垂足为点E,双曲线y=![]() (x>0)经过点D,连接MD,BD.
(x>0)经过点D,连接MD,BD.
(1)求抛物线的表达式;
(2)点N,F分别是x轴,y轴上的两点,当以M,D,N,F为顶点的四边形周长最小时,求出点N,F的坐标;
(3)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?
【答案】(1)y=﹣x2+2x+3;(2)N(![]() ,0),F(0,
,0),F(0,![]() );(3)t=9﹣2
);(3)t=9﹣2![]() .
.
【解析】
(1)由已知求出D点坐标,将点A(-1,0)和D(2,3)代入y=ax2+bx+3即可;
(2)作M关于y轴的对称点M',作D关于x轴的对称点D',连接M'D'与x轴、y轴分别交于点N、F,则以M,D,N,F为顶点的四边形周长最小即为M'D'+MD的长;
(3)设P(0,t),作△PBD的外接圆N,当⊙N与y轴相切时,∠BPD的度数最大;
解;(1)C(0,3)
∵CD⊥y,
∴D点纵坐标是3.
∵D在y=![]() 上,
上,
∴D(2,3),
将点A(﹣1,0)和D(2,3)代入y=ax2+bx+3,
∴a=﹣1,b=2,
∴y=﹣x2+2x+3;
(2)M(1,4),B(3,0),
作M关于y轴的对称点M',作D关于x轴的对称点D',连接M'D'与x轴、y轴分别交于点N、F,
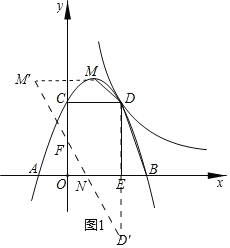
则以M,D,N,F为顶点的四边形周长最小即为M'D'+MD的长;
∴M'(﹣1,4),D'(2,﹣3),
∴M'D'直线的解析式为y=﹣![]() x+
x+![]() ,
,
∴N(![]() ,0),F(0,
,0),F(0,![]() );
);
(3)设P(0,t).
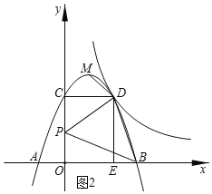
∵△PBO和△CDP都是直角三角形,
tan∠CDP=![]() ,tan∠PBO=
,tan∠PBO=![]() ,
,
令y=tan∠BPD=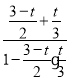 ,
,
∴yt2+t﹣3yt+6y﹣9=0,
△=﹣15y2+30y+1=0时,
y=![]() (舍)或y=
(舍)或y=![]() ,
,
∴t=![]() ﹣
﹣![]() ×
×![]() ,
,
∴t=9﹣2![]() ,
,
∴P(0,9﹣2![]() ).
).


科目:初中数学 来源: 题型:
【题目】下表中给出了变量x与ax2,ax2+bx+c之间的部分对应值(表格中的符号“…”表示该项数据已经丢失)
x | -1 | 0 | 1 |
ax | … | … | 1 |
ax+ bx + c | 7 | 2 | … |
(1)写出这条抛物线的开口方向,顶点D的坐标;并说明它的变化情况;
(2)抛物线![]() 的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
(3)在(2)的条件下,设线段BD交x轴于点C,试写出∠BAD与∠DCO的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
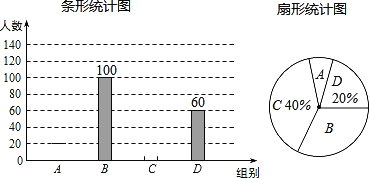
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,今年受“新冠肺炎”疫情的影响,为落实教育部“停课不停学”的要求,我市中学生进行居家线上学习,为保证广大学生的身心健康,有关部门就“你每天线上学习时在室内或室外安全区域体育锻炼时间是多少”的问题在某校开展了电话调查,随机抽查了部分学生,再根据锻炼时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如图两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人,并补全条形统计图;
(2)计算扇形统计图中A组部分所对应的扇形圆心角度数;
(3)若当天该校进行居家线上学习的学生数为1300人,请估计在当天达到国家规定体育活动时间的学生有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,4),B(﹣4,0),C(﹣1,0).
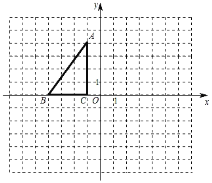
(1)△A1B1C1与△ABC关于原点O对称,画出△A1B1C1并写出点A1的坐标;
(2)△A2B2C2是△ABC绕原点O顺时针旋转90°得到的,画出△A2B2C2并写出点A2的坐标;
(3)连接OA、OA2,在△ABC绕原点O顺时针旋转90°得到的△A2B2C2的过程中,计算A变换到A2过程中的路径是多少?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备从机械厂购进甲、乙两种零件进行销售,若一个甲种零件的进价比一个乙种零件的进价多50元,用4000元购进甲种零件的数量是用1500元购进乙种零件的数量的2倍.
(1)求每个甲种零件,每个乙种零件的进价分别为多少元?
(2)这个商店甲种零件每件售价为260元,乙种零件每件售价为190元,商店根据市场需求,决定向该厂购进一批零件,且购进乙种零件的数量比购进甲种零件的数量的2倍还多4个,若本次购进的两种零件全部售出后,总获利大于2400元.求该商店本次购进甲种零件至少是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
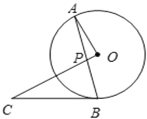
【题目】如图,AB是⊙O的弦,点C为⊙O外一点,CO⊥OA,交AB于点P,连接BC,BC=PC.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求PC的长.
(3)在(2)的条件下,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
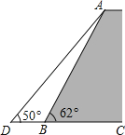
【题目】如图,某防洪堤坝长300米,其背水坡的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得加固后坡面的坡角∠ADB=50°
(1)求此时应将坝底向外拓宽多少米?(结果保留到0.01米)
(2)完成这项工程需要土石多少立方米?(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com