
 如图,在四边形ABCD的外侧,以四边形的边为边分别作四个小正方形,连接相邻的两个顶点,得到四个阴影三角形,则这四个阴影三角形的面积a、b、c、d满足( )
如图,在四边形ABCD的外侧,以四边形的边为边分别作四个小正方形,连接相邻的两个顶点,得到四个阴影三角形,则这四个阴影三角形的面积a、b、c、d满足( )| A. | a+b=c+d | B. | a2+b2=c2+d2 | C. | a+c=b+d | D. | a2+c2=b2+d2 |
分析 如图,以△ABC的边为边分别正方形ABDE,正方形ACHG,首先证明S△AEG=S△ABC,利用这个结论即可解决问题.
解答 解:如图,以△ABC的边为边分别正方形ABDE,正方形ACHG.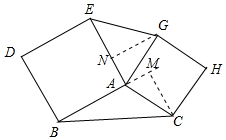
∵S△AEG=$\frac{1}{2}$•AE•GN=$\frac{1}{2}$•AE•AG•sin∠EAG,
S△ACB=$\frac{1}{2}$•AB•CM=$\frac{1}{2}$•AB•AC•sin∠CAM,
∵AB=AE,AC=AG,
∠EAG+∠BAC=180°,∠CAM+∠BAC=180°,
∴∠EAG=∠CAM,
∴S△AEG=S△ABC,
如图1中,连接AC、BD.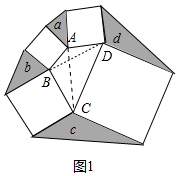
由上面的结论可知,S△ABD=a,S△BCD=c,S△ABC=b,S△ADC=d,
∵S四边形ABCD=a+c=b+d,
∴a+c=b+d,
故选C.
点评 本题考查正方形的性质、三角形的面积等知识,解题的关键是记住基本结论,利用基本结论解决问题,属于中考常考题型.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 3.2(1+x)2=3 | B. | 3.2(1-x)2=3 | C. | 3(1+x)2=3.2 | D. | 3(1-x)2=3.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向下,直线x=3,(3,2) | B. | 向下,直线x=-3,(3,2) | ||
| C. | 向上,直线x=-3,(3,2) | D. | 向下,直线x=-3,(-3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
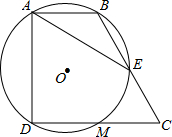 如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.
如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中CD⊥AB于点D,AC=8,BC=6,CD=$\sqrt{15}$.
如图,在△ABC中CD⊥AB于点D,AC=8,BC=6,CD=$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发,沿BC方向以每秒1cm的速度向终点C运动,当△PQC为以QC为底边的等腰三角形的时候,时间t的值为多少?
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发,沿BC方向以每秒1cm的速度向终点C运动,当△PQC为以QC为底边的等腰三角形的时候,时间t的值为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com