
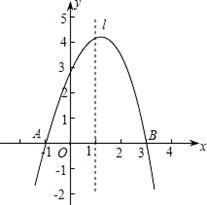
| 解:(1)将A(﹣1,0)、B(3,0)、C(0,3) 代入抛物线y=ax2+bx+c中, 得: 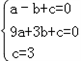 ,解得: ,解得: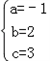 ∴抛物线的解析式:y=﹣x2+2x+3; (2)连接BC,直线BC与直线l的交点为P; 设直线BC的解析式为y=kx+b, 将B(3,0),C(0,3)代入上式, 得: 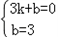 ,解得: ,解得: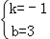 ∴直线BC的函数关系式y=﹣x+3; 当x=1时,y=2,即P的坐标(1,2); (3)抛物线的解析式为:x=﹣ 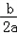 =1, =1,设M(1,m),已知A(﹣1,0)、C(0,3), 则:MA2=m2+4,MC2=m2﹣6m+10,AC2=10; ①若MA=MC,则MA2=MC2, 得:m2+4=m2﹣6m+10, 得:m=1; ②若MA=AC,则MA2=AC2, 得:m2+4=10,得:m=± 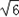 ; ;③若MC=AC,则MC2=AC2, 得:m2﹣6m+10=10, 得:m=0,m=6; 当m=6时,M、A、C三点共线,构不成三角形, 不合题意,故舍去; 综上可知,符合条件的M点存在, 且坐标为 M(1, 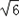 )(1,﹣ )(1,﹣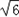 )(1,1)(1,0). )(1,1)(1,0). |
 |


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
已知抛物线y=ax2+bx+c(a>0)经过点B(12,0)和C(0,-6),对称轴为x=2.
(1)求该抛物线的解析式.
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若![]() 存在,请求出此时的时间t(秒)和点Q的运动速度;若存在,请说明理由.
存在,请求出此时的时间t(秒)和点Q的运动速度;若存在,请说明理由.
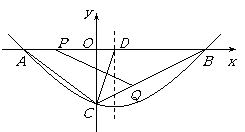 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
标;若存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
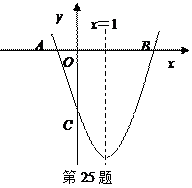 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.查看答案和解析>>
科目:初中数学 来源:2012届山东邹城北宿中学九年级3月月考数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点D(m,m+1)在第一象限的抛物线上, 求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连结BD,若点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2010-2011年浙江省嵊州市九年级上学期期末考试数学卷 题型:解答题
(本小题满分14分)
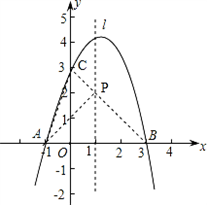
如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3)。设抛物线的顶点为D,求解下列问题:

1.(1)求抛物线的解析式和D点的坐标;
2.(2)过点D作DF∥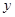 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
3.(3)能否在抛物线上找到一点Q,使△BDQ为直角三角形?若能找到,试写出Q点的坐标;若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com