
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.

【答案】(1)证明见解析(2)当∠ABC=60°时,四边形ABEF为矩形
【解析】
(1)根据旋转得出CA=CE,CB=CF,根据平行四边形的判定得出即可;
(2)根据等边三角形的判定得出△ABC是等边三角形,求出AE=BF,根据矩形的判定得出即可.
(1)∵将△ABC绕点C顺时针旋转180°得到△EFC,∴△ABC≌△EFC,∴CA=CE,CB=CF,∴四边形ABEF是平行四边形;
(2)当∠ABC=60°时,四边形ABEF为矩形,理由是:∵∠ABC=60°,AB=AC,∴△ABC是等边三角形,∴AB=AC=BC.
∵CA=CE,CB=CF,∴AE=BF.
∵四边形ABEF是平行四边形,∴四边形ABEF是矩形.


科目:初中数学 来源: 题型:
【题目】如图①,ΔABC中,AD⊥BC于点D,以A为直角顶点,分别以AB、AC为直角边,向ΔABC外作等腰RtΔABE和等腰RtΔACF,过点E、F作射线DA的垂线,垂足分别为Q、P.
(1)试探究线段EQ和FP之间的数量关系,并说明理由.
(2)如图②,若连接EF交DA的延长线于点H,由(1)中的结论你能判断EH与FH的大小关系吗?并说明理由.
(3)图②中的ΔABC与ΔAEF的面积相等吗?(直接给出结论,不需要说理)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AC∥BD,请先作图再解决问题.
(1)利用尺规完成以下作图,并保留作图痕迹.(不要求写作法)
①作BE平分∠ABD交AC于点E;
②在BA的延长线上截取AF=BA,连接EF;
(2)判断△BEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的方程x2-ax+a2-3=0至少有一个正根,则实数a的取值范围是( )
A. -2<a<2 B. ![]() <a≤2 C.
<a≤2 C. ![]() <a≤2 D.
<a≤2 D. ![]() ≤a≤2
≤a≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换,例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.現有10×10的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )
的另一个格点的运动称为一次跳马变换,例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.現有10×10的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )

A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
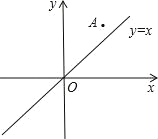
【题目】如图,已知点A(2,3)和直线y=x,
(1)点A关于直线y=x的对称点为点B,点A关于原点(0,0)的对称点为点C;写出点B、C的坐标;
(2)若点D是点B关于原点(0,0)的对称点,判断四形ABCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长为20.
(1)尺规作图,画出线段AB的垂直平分线(不写作法,保留作图痕迹);
(2)设AB的垂直平分线与BA交于点D,与BC交于点E,若AD=4,求△ACE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O是矩形ABCD的中心(对角线的交点),AB=4cm,AD=6cm.点M是边AB上的一动点,过点O作ON⊥OM,交BC于点N,设AM=x,ON=y,今天我们将根据学习函数的经验,研究函数值y随自变量x的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量x的取值范围是______;
(2)通过计算,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 2.40 | 2.24 | 2.11 | 2.03 | __ | __ | 2.11 | 2.24 | 2.40 |
请你补全表格(说明:补全表格时相关数值保留两位小数,参考数据:![]() ≈3.04,
≈3.04,![]() ≈6.09)
≈6.09)
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象.
(4)根据图象,请写出该函数的一条性质.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com