
����Ŀ��(2016����������25��)
��ͼ����֪��A������Ϊ(-2��0)��ֱ��y=-![]() +3��x�ᣬy��ֱ��ڵ�B�͵�C,����AC������ΪD��������y=ax2+bx+c��A��B��C���㣮
+3��x�ᣬy��ֱ��ڵ�B�͵�C,����AC������ΪD��������y=ax2+bx+c��A��B��C���㣮
(1)��ֱ��д��B��C��������꣬�����ߵĽ���ʽ������D�����ꣻ
(2)�������ߵĶԳ���DE���߶�BC�ڵ�E��PΪ��һ��������������һ�㣬����P��x��Ĵ��ߣ����߶�BC�ڵ�F���ı���DEFPΪƽ���ı���,���P�����ꣻ
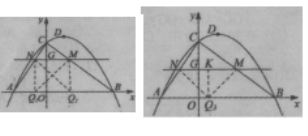
(3)����M���߶�BC�ϵ�һ���㣬����M��MN��AB����AC�ڵ�N��.Q�ӵ�B��������ÿ��l����λ���ȵ��ٶ����߶�BA���A�˶����˶�ʱ��Ϊt(��)����t(��)Ϊ��ֵʱ������QMNΪ����ֱ��������?

���𰸡���1��(1)B(4��O)��C(0��3)�������ߵĽ���ʽΪ![]() ����D������Ϊ
����D������Ϊ![]() ����2������P����Ϊ(3��
����2������P����Ϊ(3��![]() )ʱ���ı���DEFPΪƽ���ı��Σ���3����tΪ
)ʱ���ı���DEFPΪƽ���ı��Σ���3����tΪ![]() ��
��![]() ��
��![]() ʱ��������QMNΪ����ֱ�������Σ�
ʱ��������QMNΪ����ֱ�������Σ�
��������
�����������1����ֱ��y=-![]() +3�Ľ���ʽ���ɵ�B��C��������꣬���ô���ϵ����������������ߵĽ���ʽ�����������ߵĽ���ʽ���ɵ������ߵĽ���ʽ����2�����P����Ϊ
+3�Ľ���ʽ���ɵ�B��C��������꣬���ô���ϵ����������������ߵĽ���ʽ�����������ߵĽ���ʽ���ɵ������ߵĽ���ʽ����2�����P����Ϊ![]() ���F������Ϊ(m��-
���F������Ϊ(m��-![]() m+3)�������ı���DEFPΪƽ���ı��Σ���PF=DE���ɴ��з������m��ֵ�����ɵõ�P�����ꣻ��3���ֱ��Ե�M��N��QΪֱ�Ƕ������۽������.
m+3)�������ı���DEFPΪƽ���ı��Σ���PF=DE���ɴ��з������m��ֵ�����ɵõ�P�����ꣻ��3���ֱ��Ե�M��N��QΪֱ�Ƕ������۽������.
���������(1)B(4��O)��C(0��3)��
�����ߵĽ���ʽΪ![]()
����D������Ϊ![]()
(2)��x=1����![]()
���PΪ��һ��������������һ�㣬���Կ����P����Ϊ![]()
��F������Ϊ(m��-![]() m+3)�����ı���DEFPΪƽ���ı��Σ���PF=DE
m+3)�����ı���DEFPΪƽ���ı��Σ���PF=DE
��-![]() m2+
m2+![]() m+3-(-
m+3-(-![]() m+3)=
m+3)=![]()
��֮����m1=3,m2=1(�������⣬��ȥ)��
������P����Ϊ(3��![]() )ʱ���ı���DEFPΪƽ���ı��Σ�
)ʱ���ı���DEFPΪƽ���ı��Σ�
(3)���M������Ϊ(n��-![]() )��MN��y���ڵ�G��
)��MN��y���ڵ�G��
![]()
![]() ��BAC
��BAC![]()
������Q1MN=90����MN=MQ2=OGʱ��![]() ��֮��MN=2��
��֮��MN=2��
![]() ��֮��
��֮��![]()
����![]() ʱ���������
ʱ���������![]()
![]()
������MQ3N=90����Q3M=Q3Nʱ��![]() NM=Q3K=OG
NM=Q3K=OG
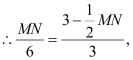 ��֮����MN=3��
��֮����MN=3��
![]()
![]() ��֮����n=2����
��֮����n=2����![]()
MN���е�K������Ϊ![]()
![]() ��
��![]()
����tΪ![]() ��
��![]() ��
��![]() ʱ��������QMNΪ����ֱ�������Σ�
ʱ��������QMNΪ����ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ˮƽ����ߣ����ýγ�Խ��Խ��ؽ����ͥ��С����������һ��С�γ�����������¼��7����ÿ����ʻ��·��(���±�)����50 kmΪ��������50 km�ļ�Ϊ������������50 km�ļ�Ϊ���������պ�50 km�ļ�Ϊ��0����
��һ�� | �ڶ��� | ������ | ������ | ������ | ������ | ������ | |
·��(km) | ��8 | ��11 | ��14 | 0 | ��16 | ��41 | ��8 |
(1)�������������ƽ��ÿ����ʻ����ǧ�ף�
(2)��ÿ����ʻ100 km��������6�������ͼ�6.2Ԫ/���������С����һ����(��30���)�����ͷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
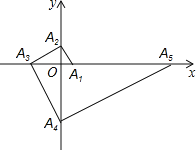
����Ŀ����ͼ����A1������Ϊ��1��0����A2��y����������ϣ��ҡ�A1A2O=30�㣬����A2��A2A3��A1A2������ΪA2����x���ڵ�A3������A3��A3A4��A2A3������ΪA3����y���ڵ�A4������A4��A4A5��A3A4������ΪA4����x���ڵ�A5������A5��A5A6��A4A5������ΪA5����y���ڵ�A6�������˹��ɽ�����ȥ�����A2016��������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ں��֡������е��ճ���Ʒ���У�����ԳƵ��У�������
A.3��B.4��C.5��D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������д�����ǣ�������
A.ƽ���ı��εĶԽ�����ƽ��B.���εĶԽ����ഹֱ
C.ͬ���ڽǻ���D.���εĶԽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
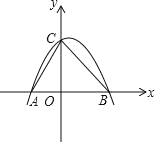
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0������A����3��0����B��5��0����C��0��5�����㣬OΪ����ԭ��
��1����������ߵĽ���ʽ��
��2������������y=ax2+bx+c��a��0������ƽ��![]() ����λ���ȣ�������ƽ��n��n��0������λ���ȵõ��������ߣ����������ߵĶ���M�ڡ�ABC�ڣ���n��ȡֵ��Χ��
����λ���ȣ�������ƽ��n��n��0������λ���ȵõ��������ߣ����������ߵĶ���M�ڡ�ABC�ڣ���n��ȡֵ��Χ��
��3�����P��y���ϣ��������OPA+��OCA=��CBA����CP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=2x2������ƽ��3����λ��������ƽ��4����λ�����������ߵĺ�������ʽΪ�� ��
A.y=2��x+3��2+4
B.y=2��x+3��2��4
C.y=2��x��3��2��4
D.y=2��x��3��2+4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=2x2��ͼ��������ƽ��2����λ��������ƽ��3����λ�õ��������ߵĽ���ʽ�ǣ� ��
A.y=2��x��2��2��3
B.y=2��x��2��2+3
C.y=2��x+2��2��3
D.y=2��x+2��2+3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com