
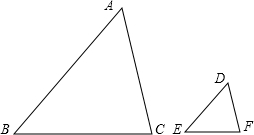
 教材第97页在证明“两边对应成比例且夹角对应相等的两个三角形相似”(如图,已知
教材第97页在证明“两边对应成比例且夹角对应相等的两个三角形相似”(如图,已知| DE |
| AB |
| DF |
| AC |
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 教材第97页在证明“两边对应成比例且夹角对应相等的两个三角形相似”(如图,已知
教材第97页在证明“两边对应成比例且夹角对应相等的两个三角形相似”(如图,已知 (AB>DE),∠A=∠D,求证:△ABC∽△DEF)时,利用了转化的数学思想,通过添设辅助线,将未知的判定方法转化为前两节课已经解决的方法(即已知两组角对应相等推得相似或已知平行推得相似).请利用上述方法完成这个定理的证明.
(AB>DE),∠A=∠D,求证:△ABC∽△DEF)时,利用了转化的数学思想,通过添设辅助线,将未知的判定方法转化为前两节课已经解决的方法(即已知两组角对应相等推得相似或已知平行推得相似).请利用上述方法完成这个定理的证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com