
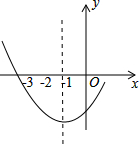 如图是二次函数y=ax2+bx-1图象的一部分,其对称轴为x=-1,且过点(-3,0),则(a+b+1)(2-a-b)=2.
如图是二次函数y=ax2+bx-1图象的一部分,其对称轴为x=-1,且过点(-3,0),则(a+b+1)(2-a-b)=2. 科目:初中数学 来源: 题型:填空题
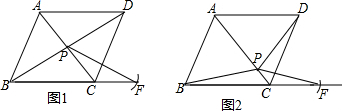
 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车:④当甲、乙两车相距50千米时,$t=\frac{5}{4}$或$\frac{15}{4}$.其中不正确的结论是③④(填序号)
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车:④当甲、乙两车相距50千米时,$t=\frac{5}{4}$或$\frac{15}{4}$.其中不正确的结论是③④(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A(△EFA与⊙O除切点外无重叠部分),延长FA交CD边于点G,则AG的长是$\frac{\sqrt{865}}{3}$.
如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A(△EFA与⊙O除切点外无重叠部分),延长FA交CD边于点G,则AG的长是$\frac{\sqrt{865}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD内接于⊙O,∠A=100°,⊙O的半径=2,则劣弧$\widehat{BD}$的长=$\frac{16π}{9}$.
如图,四边形ABCD内接于⊙O,∠A=100°,⊙O的半径=2,则劣弧$\widehat{BD}$的长=$\frac{16π}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
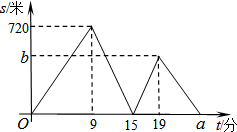 小强、小林从学校出发,沿着笔直的道路去少年宫参加书法比赛,小强步行去少年宫一段时间后,小林骑自行车去少年宫,两人均匀速前行.他们两人之间的距离s(米)与小强出发时间t(分)之间的函数关系如图.
小强、小林从学校出发,沿着笔直的道路去少年宫参加书法比赛,小强步行去少年宫一段时间后,小林骑自行车去少年宫,两人均匀速前行.他们两人之间的距离s(米)与小强出发时间t(分)之间的函数关系如图.| A. | ①② | B. | ②④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
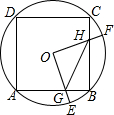 如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A、B重合),点F是$\widehat{BC}$上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A、B重合),点F是$\widehat{BC}$上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com