
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示:
(1)甲乙两地相距 千米,慢车速度为 千米/小时.
(2)求快车速度是多少?
(3)求从两车相遇到快车到达甲地时y与x之间的函数关系式.
(4)直接写出两车相距300千米时的x值.
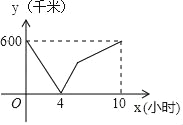
【答案】(1)600, 60;(2)快车速度是90千米/小时;(3)从两车相遇到快车到达甲地时y与x之间的函数关系式为y=150x﹣600;(4)当x=2小时或x=6小时时,两车相距300千米.
【解析】
1)由当x=0时y=600可得出甲乙两地间距,再利用速度=两地间距÷慢车行驶的时间,即可求出慢车的速度;
(2)设快车的速度为a千米/小时,根据两地间距=两车速度之和×相遇时间,即可得出关于a的一元一次方程,解之即可得出结论;
(3)分别求出快车到达甲地的时间及快车到达甲地时两车之间的间距,根据函数图象上点的坐标,利用待定系数法即可求出该函数关系式;
(4)利用待定系数法求出当0≤x≤4时y与x之间的函数关系式,将y=300分别代入0≤x≤4时及4≤x≤![]() 时的函数关系式中求出x值,此题得解.
时的函数关系式中求出x值,此题得解.
(1)∵当x=0时,y=600,
∴甲乙两地相距600千米.
600÷10=60(千米/小时).
故答案为:600;60.
(2)设快车的速度为a千米/小时,
根据题意得:4(60+a)=600,
解得:a=90.
答:快车速度是90千米/小时.
(3)快车到达甲地的时间为600÷90=![]() (小时),
(小时),
当x=![]() 时,两车之间的距离为60×
时,两车之间的距离为60×![]() =400(千米).
=400(千米).
设当4≤x≤![]() 时,y与x之间的函数关系式为y=kx+b(k≠0),
时,y与x之间的函数关系式为y=kx+b(k≠0),
∵该函数图象经过点(4,0)和(![]() ,400),
,400),
∴ ,解得:
,解得:![]() ,
,
∴从两车相遇到快车到达甲地时y与x之间的函数关系式为y=150x﹣600.
(4)设当0≤x≤4时,y与x之间的函数关系式为y=mx+n(m≠0),
∵该函数图象经过点(0,600)和(4,0),
∴![]() ,解得:
,解得:![]() ,
,
∴y与x之间的函数关系式为y=﹣150x+600.
当y=300时,有﹣150x+600=300或150x﹣600=300,
解得:x=2或x=6.
∴当x=2小时或x=6小时时,两车相距300千米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
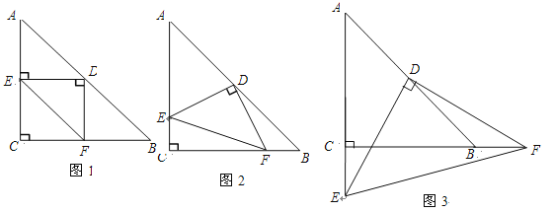
【题目】 已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证![]() .当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,
.当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学采用随机的方式对学生掌握安全知识的情况进行测评,并按成绩高低分成优、良、中、差四个等级进行统计,绘制了下面两幅尚不完整的统计图.请根据有关信息解答:
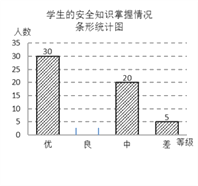
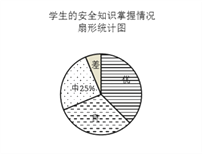
(1)接受测评的学生共有________人,扇形统计图中“优”部分所对应扇形的圆心角为________°,并补全条形统计图;
(2)若该校共有学生1200人,请估计该校对安全知识达到“良”程度的人数;
(3)测评成绩前五名的学生恰好3个女生和2个男生,现从中随机抽取2人参加市安全知识竞赛,请用树状图或列表法求出抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.

A. 1 B. 2 C. 3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=8,点P为AB的中点,E为BC上一动点,过P点作FP⊥PE交AC于F点,经过P、E、F三点确定⊙O.
(1)试说明:点C也一定在⊙O上.
(2)点E在运动过程中,∠PEF的度数是否变化?若不变,求出∠PEF的度数;若变化,说明理由.
(3)求线段EF的取值范围,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 希望小学初一年级的![]() 名同学中,至少有两个生日相同的概率是
名同学中,至少有两个生日相同的概率是![]()
B. 在投掷骰子时,连投两次点数相同的概率与连投两次点数都为![]() 的概率相等
的概率相等
C. 我们小组共![]() 名同学,他们中肯定有两人在同一月过生日
名同学,他们中肯定有两人在同一月过生日
D. 一个游戏的中奖率是![]() ,买
,买![]() 张奖券,一定会中奖
张奖券,一定会中奖
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com