
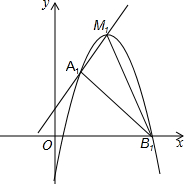
 已知:抛物线Ck:y=-x2+2kx-k2+k+1(k=1,2,3…,k为正整数),抛物线Ck的顶点为Mk.
已知:抛物线Ck:y=-x2+2kx-k2+k+1(k=1,2,3…,k为正整数),抛物线Ck的顶点为Mk.分析 (1)由y=-x2+2kx-k2+k+1=-(x-k)2+k+1,可得顶点Mk(k,k+1),由此不难解决问题;
(2)抛物线Ck的顶点为Mk在同一条直线上,由顶点Mk(k,k+1),可知顶点Mk,在直线y=x+1上;
(3)利用方程组求出Ak、Ak+1的坐标即可解决问题;
(4)分两种情形,求出点Bk的坐标,利用待定系数法,转化为方程解决问题即可;
解答 (1)解:由y=-x2+2kx-k2+k+1=-(x-k)2+k+1,可得顶点Mk(k,k+1),
∴k=1时,M1(1,2),k=2时,M2(2,3),
故答案分别为(1,2),(2,3).
(2)解:抛物线Ck的顶点为Mk在同一条直线上,
∵顶点Mk(k,k+1),
∴顶点Mk,在直线y=x+1上.
(3)证明:由$\left\{\begin{array}{l}{y=-(x-k)^{2}+k+1}\\{y=x+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=k}\\{y=k+1}\end{array}\right.$或$\left\{\begin{array}{l}{x=k-1}\\{y=k}\end{array}\right.$,
∴Ak(k-1,k),
∴Ak+1(k,k+1),
∵Mk(k,k+1),
∴Mk与Ak+1重合;
(4)观察图象可知当△AkBkMk是直角三角形时,有两种可能:
①当BkAk⊥AkMk时,
∵直线l的解析式为y=x+1,
∴∠AkBkO=45°,
∵Ak(k-1,k),
∴Bk(2k-1,0),
把Bk(2k-1,0),代入y=-x2+2kx-k2+k+1得到,-(2k-1)2+2k(2k-1)-k2+k+1=0,
解得k=3或0(舍弃),
②当BkMk⊥AkMk时,
∵直线l的解析式为y=x+1,
∴∠MkBkO=45°,
∵Mk(k,k+1),
∴Bk(2k+1,0),
把Bk(2k+1,0),代入y=-x2+2kx-k2+k+1得到,-(2k+1)2+2k(2k+1)-k2+k+1=0,
解得K=-1或0(均不符合题意舍弃),
综上所述,满足条件的k的值为3.
点评 本题考查二次函数综合题、一次函数的应用、直角三角形的性质、两直线垂直的条件等知识,解题的关键是辛苦利用此时解决问题,学会用分类讨论的思想思考问题,学会构建一次函数,利用方程组确定交点坐标,属于中考压轴题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
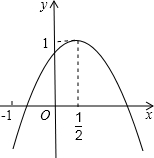 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
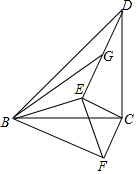 如图,在等腰直角△BCD中,∠BCD=90°,BC=CD,E为△BCD内一点,且CE⊥DE,DE=2CE,将△CDE绕点C逆时针旋转90°得到△CBF,连接EF、BE,G为DE的中点,连接BG.如果△BDG的面积为1cm2,那么BG的长度为$\sqrt{10}$cm.
如图,在等腰直角△BCD中,∠BCD=90°,BC=CD,E为△BCD内一点,且CE⊥DE,DE=2CE,将△CDE绕点C逆时针旋转90°得到△CBF,连接EF、BE,G为DE的中点,连接BG.如果△BDG的面积为1cm2,那么BG的长度为$\sqrt{10}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “打开电视,正在播放《动物世界》”是必然事件 | |
| B. | 某种彩票的中奖概率为$\frac{1}{1000}$,说明每买1000张彩票,一定有一张中奖 | |
| C. | 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为$\frac{1}{2}$ | |
| D. | 投掷两枚普通的正方体骰子,掷得两个6的概率是$\frac{1}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com