
分析 (1)根据绝对值、特殊角的三角函数值、零指数幂可以解答本题;
(2)根据分式的除法和减法可以解答本题.
解答 解:(1)|1-$\sqrt{3}$|-$\sqrt{12}$+2cos30°-20170
=$\sqrt{3}-1-2\sqrt{3}+2×\frac{\sqrt{3}}{2}-1$
=$\sqrt{3}-1-2\sqrt{3}+\sqrt{3}-1$
=-2;
(2)1-$\frac{x-2}{x}$÷$\frac{{x}^{2}-4}{{x}^{2}+x}$
=$1-\frac{x-2}{x}•\frac{x(x+1)}{(x+2)(x-2)}$
=1-$\frac{x+1}{x+2}$
=$\frac{x+2-x-1}{x+2}$
=$\frac{1}{x+2}$.
点评 本题考查分式的混合运算、绝对值、特殊角的三角函数值、零指数幂,解答本题的关键是明确它们各自的计算方法.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:填空题
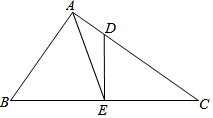 如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.
如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.
学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方式 | 频数 | 百分比 |
| 网络 | 23 | 46% |
| 电视 | ||
| 报纸 | 8% | |
| 其他 | 15 | |
| 合计 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
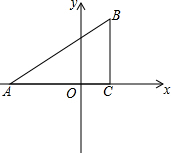 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=$\frac{3}{4}$AC
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=$\frac{3}{4}$AC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com