
 如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s).
如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s).分析 (1)根据正六边形ABCDEF内接于⊙O,可以得到正六边形的各边相等、各个内角相等,由点P,Q同时分别从A,D两点出发,以1cm/s速度,运动时间为t,可以得到BP与QE,PE与BQ的关系,从而可以证得结论;
(2)①根据菱形的性质可以得到菱形的四条边都相等,从而可以得到所用的时间;
②根据矩形的性质,可以分别得到t为多少时,四边形PBQE为矩形.
解答 (1)证明:∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度,运动时间为t(s),
∴AP=DQ=t,则PF=QC=4-t,
在△ABP和△DEQ中
$\left\{\begin{array}{l}{AB=DE}\\{∠A=∠D}\\{AP=DQ}\end{array}\right.$
∴△ABP≌△DEQ(SAS)
∴BP=EQ,
同理可证,PE=QB,
∴四边形PEQB是平行四边形.
(2)解:①当四边形PBQE为菱形时,PB=PE=EQ=QB,
∴△ABP≌△DEQ≌△PFE≌△QCB,
∴AP=PF=DQ=QC,
即t=4-t,得t=2,
故答案为:2;
②当t=0时,∠EPF=∠PEF=30°,
∴∠BPE=120°-30°=90°,
∴此时四边形PBQE为矩形;
当t=4时,∠ABP=∠APB=30°,
∴∠BPE=120°-30°=90°,
∴此时四边形PBQE为矩形.
故答案为:0或4.
点评 本题考查圆的综合题、平行四边形的判定、菱形的性质、矩形的性质,解题的关键是明确题意,利用数形结合的思想,找出所要证明的结论需要的条件.


科目:初中数学 来源: 题型:解答题
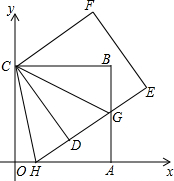 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+ax+8(a≠0)于x轴从左到右交于点A,B于y轴交于点C于直线y=kx+b交于点c和点D(m,5),tan∠DCO=1
如图,抛物线y=-x2+ax+8(a≠0)于x轴从左到右交于点A,B于y轴交于点C于直线y=kx+b交于点c和点D(m,5),tan∠DCO=1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC为等边三角形,G,H分别从C,A出发,以等速沿CA,AB运动,连CH,BG交于F.
△ABC为等边三角形,G,H分别从C,A出发,以等速沿CA,AB运动,连CH,BG交于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数1.8与1.80表示的意义不同 | B. | 0.0200精确到万分位 | ||
| C. | 2.0万精确到万位 | D. | 1.0×104精确到千位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com