
����Ŀ����ƽ��ֱ������ϵ�У�������y��mx2��2mx��3m��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C������AC��BC������OBC��BC���ڵ�ֱ�߷��ۣ��õ���DBC������OD��
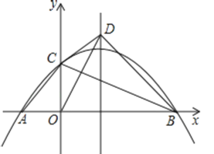
��1����A�������� ������B�������� ����
��2����ͼ������D���������ߵĶԳ����ϣ�����x���Ϸ����������ߵĽ���ʽ��
��3������OBD�����ΪS1����OAC�����ΪS2����S1��![]() S2����m��ֵ��
S2����m��ֵ��
���𰸡���1��(��1��0)��(3��0)����2��y����![]() x2+
x2+![]() x+
x+![]() ����3����
����3����![]()
��������
��1�������ߵı���ʽΪ��y��m��x2��2x��3����m��x+1����x��3����������⣻
��2��֤����CPD�ס�DQB��������⣻
��3��S2��S��AOC��![]() ��1������3m����-
��1������3m����-![]() m����S1��S��BOD��
m����S1��S��BOD��![]() ��DO��MB��OM��MB����S1��
��DO��MB��OM��MB����S1��![]() S2�������.
S2�������.
��1�������ߵı���ʽΪ��y��m��x2��2x��3����m��x+1����x��3����
�ʵ�A��B������ֱ�Ϊ������1��0������3��0����
�ʴ�Ϊ������1��0������3��0����
��2������B��y���ƽ����BQ������D��x���ƽ���߽�y���ڵ�P����BQ�ڵ�Q��
�裺D��1��n������C��0����3m����
�ߡ�CDP+��PDC��90������PDC+��QDB��90����
���QDB����DCP��
�֡ߡ�CPD����BQD��90����
���CPD�ס�DQB��
��![]() ,
,
����CP��n+3m��DQ��3��1��2��PD��1��BQ��n��CD����3m��BD��3��
��������ֵ�������ʽ����ã�m����![]() ��
��
��m��0����m����![]() ��
��
�������ߵı���ʽΪ��y����![]() x2+
x2+![]() x+
x+![]() ��
��
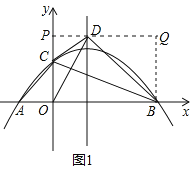
��3��y��m��x2��2x��3����m��x+1����x��3����
��C��0����3m����CO����3m��
��A����1��0����B��3��0����
��AB��4��
��S2��S��AOC��![]() ��1������3m������
��1������3m������![]() m��
m��
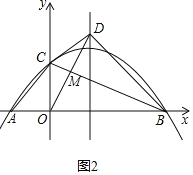
��OD��BC�ڵ�M��
����Գ��ԣ�BC��OD��OD��2OM��
��Rt��COB��BC��![]() ,
,
��������ã�OM�� ![]() ,
,
��tan��COB��![]() ����m����cos��COB��
����m����cos��COB��![]() ,
,
MB��OBcos��COB��![]() ,
,
��S1��S��BOD��![]() ��DO��MB��OM��MB����
��DO��MB��OM��MB����![]() ,
,
��S1��![]() S2��
S2��
��m2+1��![]() ��m��0����
��m��0����
��m����![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��AD���е㣬�ӳ�CE��BA���ڵ�F������AC��DF��
��1����֤���ı���ACDF��ƽ���ı��Σ�
��2����CFƽ�֡�BCDʱ��д��BC��CD��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �ڽ��ڰ�Բ
�ڽ��ڰ�Բ![]() ��
��![]() Ϊֱ����
Ϊֱ����![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�F.��
�ڵ�F.��![]() ��
��![]() ����
����![]() �ij�Ϊ ��������
�ij�Ϊ ��������
A.8B.10C.15D.24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ����
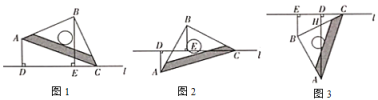
��ͼ1����һ������ֱ�����dz�![]() �Ķ���
�Ķ���![]() ������ֱ��
������ֱ��![]() �ϣ�
�ϣ�![]() ��
��![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
�۲췢�֣�
��1����ͼ1����![]() ��
��![]() �������ֱ��
�������ֱ��![]() ���Ϸ�ʱ��
���Ϸ�ʱ��
�ٲ²��߶�![]() ��
��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
��ֱ��д���߶�![]() ��
��![]() ��
��![]() ��������ϵ��
��������ϵ��
����֤����
��2��������ֱ�����dz�![]() ���ŵ�
���ŵ�![]() ��ʱ����ת��ͼ2λ��ʱ���߶�
��ʱ����ת��ͼ2λ��ʱ���߶�![]() ��
��![]() ��
��![]() ����������������ϵ����д����IJ��룬��д��֤�����̣�
����������������ϵ����д����IJ��룬��д��֤�����̣�
�ع�̽����
��3��������ֱ�����ó�![]() ���ŵ�
���ŵ�![]() ������ת��ͼ3λ��ʱ��
������ת��ͼ3λ��ʱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ����ֱ��д��
����ֱ��д��![]() �ij��ȣ�
�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����ʡ�����У�Ϊ�˽�ijУѧ���Ŀ�����Ȥ���������ij����С����������Ķ������������������鷨�������������ĸ�ѡ�����������ķ��������˸�У����ѧ���Ŀ�����Ȥ���������ÿ��ѧ������ѡһ����ֻ��ѡһ��������ݵ���������������ͳ��ͼ��
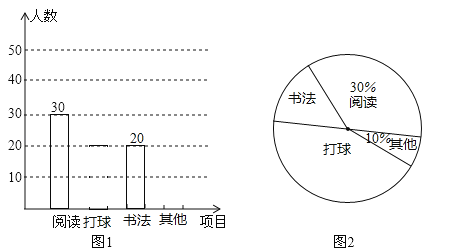
����ͳ��ͼ���ṩ����Ϣ������������⣺
��1�����γ��������е����������� ��
��2����ȫ����ͳ��ͼ��
��3����У����2000��ѧ���������ͳ�ƽ�����Ƹ�У������Ȥ����Ϊ����������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
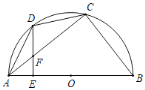
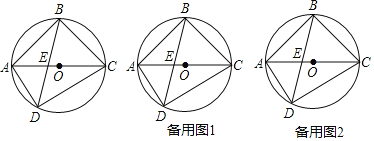
����Ŀ����ͼ���ı���ABCD�ڽ�����O��ACΪֱ����AC��BD���ڵ�E��AB��BC��
��1�����ADB�Ķ�����
��2����B��AD��ƽ���ߣ���AC��F�����ж��߶�EA��CF��EF֮������ĵ�����ϵ����˵�����ɣ�
��3���ڣ�2�������¹�E��F�ֱ���AB��BC�Ĵ��ߣ�����ֱ�ΪG��H������GH����BO��M����AG��3��S�ı���AGMO��S�ı���CHMO��8��9������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���мס������ֿͳ���2�����ֿͳ���3�����ֿͳ������ؿ���Ϊ180�ˣ�1�����ֿͳ���2�����ֿͳ������ؿ���Ϊ105�ˣ�
��1������1�����ֿͳ���1�����ֿͳ����ؿ����ֱ�Ϊ�����ˣ�
��2��ijѧУ��֯240��ʦ�����������������üס������ֿͳ���6����һ�ν�ȫ��ʦ���͵�ָ���ص㣮��ÿ�����ֿͳ������Ϊ400Ԫ��ÿ�����ֿͳ������Ϊ280Ԫ����������ʡ���õ���������������ͷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
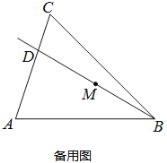
����Ŀ����ͼ���ڡ�ABC�У�![]() ��tanA=3����ABC=45��������BD��������BA�غϵ�λ�ÿ�ʼ���Ƶ�B��˳ʱ�뷽����ת��������BC�غ�ʱ��ֹͣ��ת������BD���߶�AC�ཻ�ڵ�D����M���߶�BD���е㣮
��tanA=3����ABC=45��������BD��������BA�غϵ�λ�ÿ�ʼ���Ƶ�B��˳ʱ�뷽����ת��������BC�غ�ʱ��ֹͣ��ת������BD���߶�AC�ཻ�ڵ�D����M���߶�BD���е㣮
��1�����߶�BC�ij���
��2���ٵ���D���A����C���غ�ʱ������D��DE��AB�ڵ�E��DF��BC�ڵ�F������ME��MF��������BD��ת�Ĺ����У���EMF�Ĵ�С�Ƿ����仯�������䣬���EMF�Ķ��������仯����˵�����ɣ�
���ڢٵ������£�����EF��ֱ��д����EFM�������Сֵ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
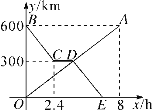
����Ŀ�������ͽγ��ֱ�Ӽס�������ͬʱ��������ͬһ��·������У��γ�����2.4h����Ϣ��ֱ���������������ԭ�ٶȼ�����ʻ�����������xh�������γ��ֱ����y1km��y2km�ĵط���ͼ�е��߶�OA������BCDE�ֱ��ʾy1��y2��x֮��ĺ�����ϵ��
(1)���D�����꣬�����͵�D��ʵ�����壻
(2)���߶�DE����ֱ�ߵĺ�������ʽ��
(3)����������________hʱ���������200km��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com