
·ÖĪö £Ø1£©Ö±½Óøł¾ŻĢāŅāŹŪ¼ŪĆæÕĒ1ŌŖĆæŌĀŅŖÉŁĀō10¼ž£»ŹŪ¼ŪĆæĻĀ½µ1ŌŖĆæŌĀŅŖ¶ąĀō20¼ž£¬½ų¶ųµĆ³öµČĮæ¹ŲĻµ£»
£Ø2£©ĄūÓĆĆ漞ĄūČó”ĮĻśĮæ=×ÜĄūČ󣬽ų¶ųĄūÓĆÅä·½·ØĒó³ö¼“æÉ£»
£Ø3£©ĄūÓĆŗÆŹżĶ¼Ļó½įŗĻŅ»ŌŖ¶ž“Ī·½³ĢµÄ½ā·ØµĆ³ö·ūŗĻĢāŅāµÄ“š°ø£®
½ā“š ½ā£ŗ£Ø1£©ÓÉĢāŅāæÉµĆ£ŗy=$\left\{\begin{array}{l}{300-10x}&{£Ø0”Üx”Ü30£©}\\{300-20x}&{£Ø-20”Üx£¼0£©}\end{array}\right.$£»
£Ø2£©ÓÉĢāŅāæÉµĆ£ŗw=$\left\{\begin{array}{l}{£Ø20+x£©£Ø300-10x£©}&{£Ø0”Üx”Ü30£©}\\{£Ø20+x£©£Ø300-20x£©}&{£Ø-20”Üx£¼0£©}\end{array}\right.$£¬
»Æ¼ņµĆ£ŗw=$\left\{\begin{array}{l}{-10{x}^{2}+100x+6000}&{£Ø0”Üx”Ü30£©}\\{-20{x}^{2}-100x+6000}&{£Ø-20”Üx£¼0£©}\end{array}\right.$£¬
¼“w=$\left\{\begin{array}{l}{-10£Øx-5£©^{2}+6250}&{£Ø0”Üx”Ü30£©}\\{-20£Øx+\frac{5}{2}£©^{2}+6125}&{£Ø-20”Üx£¼0£©}\end{array}\right.$£¬
ÓÉĢāŅāæÉÖŖxӦȔÕūŹż£¬¹Źµ±x=-2»ņx=-3Ź±£¬w£¼6125£¬
x=5Ź±£¬W=6250£¬
¹Źµ±ĻśŹŪ¼ŪøńĪŖ65ŌŖŹ±£¬ĄūČó×ī“ó£¬×ī“óĄūČóĪŖ6250ŌŖ£»
£Ø3£©ÓÉĢāŅāw”Ż6000£¬ČēĶ¼£¬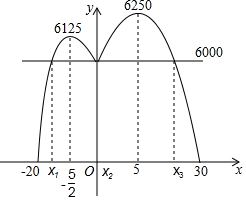
Įīw=6000£¬
½«w=6000“ųČė-20”Üx£¼0Ź±¶ŌÓ¦µÄÅ×ĪļĻß·½³Ģ£¬¼“6000=-20£Øx+$\frac{5}{2}$£©2+6125£¬
½āµĆ£ŗx1=-5£¬
½«w=6000“ųČė0”Üx”Ü30Ź±¶ŌÓ¦µÄÅ×ĪļĻß·½³Ģ£¬¼“6000=-10£Øx-5£©2+6250£¬
½āµĆx2=0£¬x3=10£¬
×ŪÉĻæÉµĆ£¬-5”Üx”Ü10£¬
¹Ź½«ĻśŹŪ¼ŪøńæŲÖĘŌŚ55ŌŖµ½70ŌŖÖ®¼ä£Øŗ¬55ŌŖŗĶ70ŌŖ£©²ÅÄÜŹ¹ĆæŌĀĄūČó²»ÉŁÓŚ6000ŌŖ£®
µćĘĄ “ĖĢāÖ÷ŅŖæ¼²éĮĖ¶ž“ĪŗÆŹżµÄÓ¦ÓĆŅŌ¼°Åä·½·ØĒ󶞓ĪŗÆŹż×īÖµµČÖŖŹ¶£¬ĄūÓĆŗÆŹżĶ¼ĻóµĆ³öxµÄȔֵ·¶Ī§ŹĒ½āĢā¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ½ā²»µČŹ½×é£ŗ$\left\{{\begin{array}{l}{\frac{1-2x}{3}”Üx+2}\\{2x+2£¾2£Ø{2x-1}£©}\end{array}}\right.$£®°ŃĖüµÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£¬²¢Š“³öÕāøö²»µČŹ½×éµÄÕūŹż½ā£®
½ā²»µČŹ½×é£ŗ$\left\{{\begin{array}{l}{\frac{1-2x}{3}”Üx+2}\\{2x+2£¾2£Ø{2x-1}£©}\end{array}}\right.$£®°ŃĖüµÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£¬²¢Š“³öÕāøö²»µČŹ½×éµÄÕūŹż½ā£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
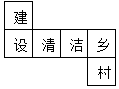 ČēĶ¼ŹĒŅ»øöŠ”Õż·½ĢåµÄÕ¹æŖĶ¼£¬°ŃÕ¹æŖĶ¼ÕŪµž³ÉŠ”Õż·½Ģåŗó£¬ÓŠ”°½Ø”±×ÖŅ»ĆęµÄĻą¶ŌĆęÉĻµÄ×ÖŹĒ£Ø””””£©
ČēĶ¼ŹĒŅ»øöŠ”Õż·½ĢåµÄÕ¹æŖĶ¼£¬°ŃÕ¹æŖĶ¼ÕŪµž³ÉŠ”Õż·½Ģåŗó£¬ÓŠ”°½Ø”±×ÖŅ»ĆęµÄĻą¶ŌĆęÉĻµÄ×ÖŹĒ£Ø””””£©| A£® | Ēå | B£® | ½ą | C£® | Ļē | D£® | “å |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
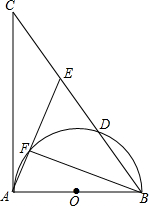 ČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻBAC=90”ć£¬ŅŌABĪŖÖ±¾¶µÄ°ėŌ²O½»BC±ßÓŚµćD£¬µćEŌŚBC±ßÉĻ£¬ĒŅAE=AB£¬Į¬½įAE½»°ėŌ²OÓŚµćF£¬Į¬½įBF£®
ČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻBAC=90”ć£¬ŅŌABĪŖÖ±¾¶µÄ°ėŌ²O½»BC±ßÓŚµćD£¬µćEŌŚBC±ßÉĻ£¬ĒŅAE=AB£¬Į¬½įAE½»°ėŌ²OÓŚµćF£¬Į¬½įBF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬AB”ĪCD£¬AE”¢DF·Ö±šŹĒ”ĻBAD”¢”ĻCDAµÄ½ĒĘ½·ÖĻߣ¬ÄĒĆ“AEÓėDFŹĒ·ńĘ½ŠŠ£æĒėĖµĆ÷ĄķÓÉ£®
ČēĶ¼£¬AB”ĪCD£¬AE”¢DF·Ö±šŹĒ”ĻBAD”¢”ĻCDAµÄ½ĒĘ½·ÖĻߣ¬ÄĒĆ“AEÓėDFŹĒ·ńĘ½ŠŠ£æĒėĖµĆ÷ĄķÓÉ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com