
【题目】如图,在矩形ABCD中,AD= ![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
A.2个
B.3个
C.4个
D.5个
【答案】C
【解析】∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE= ![]() AB,
AB,
∵AD= ![]() AB,
AB,
∴AE=AD,
在△ABE和△AHD中,
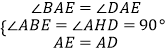 ,
,
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED= ![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB= ![]() (180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
(180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,
 ,
,
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE﹣AH=BC﹣CD,
∴BC﹣CF=BC﹣(CD﹣DF)=BC﹣(CD﹣HE)=(BC﹣CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④共4个.
所以答案是:C.
【考点精析】根据题目的已知条件,利用角平分线的性质定理和矩形的性质的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;矩形的四个角都是直角,矩形的对角线相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,花果山上有两只猴子在一棵树CD上的点B处,且BC=5m,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树10m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处.已知两只猴子所经过的路程相等,设BD为xm.
(1)请用含有x的整式表示线段AD的长为______m;
(2)求这棵树高有多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于度.(用含n的代数式表示,n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A,B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同,销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系式yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系式yB=﹣x+14.
(1)求A、B两种型号的汽车的进货单价;
(2)已知A型汽车的售价比B型汽车的售价高2万元/台,设B型汽车售价为t万元/台.每周销售这两种车的总利润为W万元,求W与t的函数关系式,A、B两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年西宁市高中招生体育考试测试管理系统的运行,将测试完进行换算统分改为计算机自动生成,现场公布成绩,降低了误差,提高了透明度,保证了公平.考前张老师为了解全市初三男生考试项目的选择情况(每人限选一项),对全市部分初三男生进行了调查,将调查结果分成五类:A、实心球(2kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)将上面的条形统计图补充完整;
(2)假定全市初三毕业学生中有5500名男生,试估计全市初三男生中选50米跑的人数有多少人?
(3)甲、乙两名初三男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com