
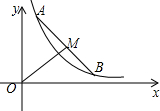
 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$-1 |
分析 设A(a,$\frac{2}{a}$),B(b,$\frac{2}{b}$),先利用线段中点坐标公式得到M($\frac{a+b}{2}$,$\frac{1}{a}$+$\frac{1}{b}$),则利用两点间的距离公式得到(a-b)2+($\frac{2}{a}$-$\frac{2}{b}$)2=16,变形为a2+b2+$\frac{4}{{a}^{2}}$+$\frac{4}{{b}^{2}}$=16+2ab+$\frac{8}{ab}$,由于OM2=($\frac{a+b}{2}$)2+($\frac{1}{a}$+$\frac{1}{b}$)2,然后根据代数式的变形得到OM2=8+($\sqrt{ab}$-$\frac{2}{\sqrt{ab}}$)2,于是可判断OM的最小值为2$\sqrt{2}$.
解答 解:设A(a,$\frac{2}{a}$),B(b,$\frac{2}{b}$),
∵M点为AB的中点,
∴M($\frac{a+b}{2}$,$\frac{1}{a}$+$\frac{1}{b}$),
∵AB=4,
∴(a-b)2+($\frac{2}{a}$-$\frac{2}{b}$)2=16,
即a2+b2-2ab+$\frac{4}{{a}^{2}}$+$\frac{4}{{b}^{2}}$-$\frac{8}{ab}$=16,
∴a2+b2+$\frac{4}{{a}^{2}}$+$\frac{4}{{b}^{2}}$=16+2ab+$\frac{8}{ab}$,
∴OM2=($\frac{a+b}{2}$)2+($\frac{1}{a}$+$\frac{1}{b}$)2=$\frac{1}{4}$(a2+2ab+b2)+$\frac{1}{{a}^{2}}$+$\frac{2}{ab}$+$\frac{1}{{b}^{2}}$
=$\frac{1}{4}$(a2+b2+$\frac{4}{{a}^{2}}$+$\frac{4}{{b}^{2}}$)+$\frac{1}{2}$ab+$\frac{2}{ab}$
=4+$\frac{1}{2}$ab+$\frac{2}{ab}$+$\frac{1}{2}$ab+$\frac{2}{ab}$
=4+ab+$\frac{4}{ab}$,
=8+($\sqrt{ab}$-$\frac{2}{\sqrt{ab}}$)2,
∴OM2≥8,
∴OM的最小值为2$\sqrt{2}$.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.解决本题的关键是运用两点间的距离公式.


科目:初中数学 来源: 题型:解答题
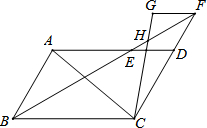 ?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.
?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
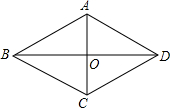 如图,四边形ABCD是菱形,对角线AC、BD相交于O,如果菱形的周长是40cm,它的一条对角线AC长10cm,
如图,四边形ABCD是菱形,对角线AC、BD相交于O,如果菱形的周长是40cm,它的一条对角线AC长10cm,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
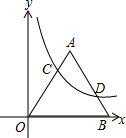 在平面直角坐标系中,等边三角形OAB中OB在x轴上,点A在第一象限,双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C,交AB于点D,若OC:BD=2:1,则OB=5.
在平面直角坐标系中,等边三角形OAB中OB在x轴上,点A在第一象限,双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C,交AB于点D,若OC:BD=2:1,则OB=5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系x0y中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=0C3,OA3=OC4…,则依此规律,点A2015的横坐标为-4×$(\frac{4}{3})^{1006}$.
如图,在平面直角坐标系x0y中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=0C3,OA3=OC4…,则依此规律,点A2015的横坐标为-4×$(\frac{4}{3})^{1006}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
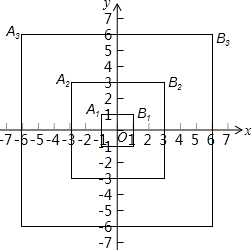 如图,第一个正方形的顶点A1(-1,1),B1(1,1);第二个正方形的顶点A2(-3,3),B2(3,3);第三个正方形的顶点A3(-6,6),B3(6,6),按顺序取点A1,B2,A3,B4,A5,B6…,则第10个点应取点B10,其坐标为(55,55),第2n-1(n为正整数)个点应取点A2n-1,其坐标为(-n(2n-1),n(2n-1)).
如图,第一个正方形的顶点A1(-1,1),B1(1,1);第二个正方形的顶点A2(-3,3),B2(3,3);第三个正方形的顶点A3(-6,6),B3(6,6),按顺序取点A1,B2,A3,B4,A5,B6…,则第10个点应取点B10,其坐标为(55,55),第2n-1(n为正整数)个点应取点A2n-1,其坐标为(-n(2n-1),n(2n-1)).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则:
如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知Rt△ABC中,∠BAC=90°,M为AC的中点,N为BM中点,AN延长线交BC于P,过P作PQ∥AB交BM于Q.求证:
已知Rt△ABC中,∠BAC=90°,M为AC的中点,N为BM中点,AN延长线交BC于P,过P作PQ∥AB交BM于Q.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com