
【题目】如图,E,F分别是正方形ABCD的边CD,AD上的点,CE=DF,AE,BF相交于点O.下列结论:①AE=BF;②AE⊥BF;③△ABF与△DAE成中心对称.其中,正确的结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
【答案】C
【解析】
根据正方形的性质及已知条件易证△ABF≌△DAE,根据全等三角形的性质即可判定①正确;再根据∠DAE+∠BAO=90°,∠ABF+∠BAO=90°,求得∠AOB=90°,即可判定②正确;利用反证法证明③错误;利用中心对称的性质判定④错误.
在正方形ABCD中,∠BAF=∠D=90°,AB=AD=CD,
∵CE=DF,
∴AD-DF=CD-CE,
即AF=DE,
在△ABF和△DAE中,
 ,
,
∴△ABF≌△DAE(SAS),
∴AE=BF,∠ABF=∠DAE,
故①正确;
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
在△ABO中,∠AOB=180°-(∠ABF+∠BAO)=180°-90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
所以,假设不成立,AO≠OE,故③错误;
连接AD、BA、FE,三条直线不相交于一点,所以△ABF与△DAE不成中心对称.
综上,正确的结论为①②.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.
(1)求证:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用直尺和圆规作一个角∠A′O′B′,等于已知角∠AOB,能得出∠A′O′B′=∠AOB的依据是( )

A.SASB.ASAC.AASD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在△ABC中,∠C=90°,AC=BC,D是边BC上一点(点D不与点B,C重合).连接AD,将AD绕着点D逆时针旋转90°,得到DE,连接BE,过点D作DF∥AC交AB于点F,可知△ADF≌△EDB,则∠ABE的大小为________.
探究:如图②,在△ABC中,∠C=α(0°<α<90°),AC=BC,D是边BC上一点(点D不与点B,C重合),连接AD,将AD绕着点D逆时针旋转α,得到DE,连接BE,求证:∠ABE=α.
应用:设图②中的α=60°,AC=2.当△ABE是直角三角形时,AE=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。

(1)①求证图1中△ADC≌△CEB;②证明DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请说明DE=AD-BE的理由;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由)。
查看答案和解析>>
科目:初中数学 来源: 题型:
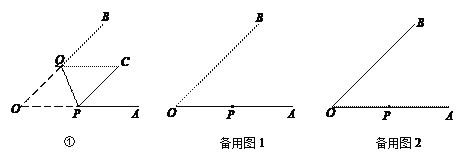
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2 cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处.
(1)①当PC∥QB时,OQ= cm;
②在OB上找一点Q,使PC⊥QB(尺规作图,保留作图痕迹);
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com