
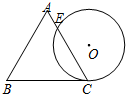
 如图,一个边长为4cm的等边三角形的高与ABC与⊙O直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为3cm.
如图,一个边长为4cm的等边三角形的高与ABC与⊙O直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为3cm. 分析 连接OC,并过点O作OF⊥CE于F,求出等边三角形的高即可得出圆的直径,继而得出OC的长度,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长
解答 解:连接OC,并过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为4cm,
∴△ABC的高为2$\sqrt{3}$cm,
∴OC=$\sqrt{3}$cm,
又∵∠ACB=60°,
∴∠OCF=30°,
在Rt△OFC中,可得FC=$\frac{3}{2}$cm,
即CE=2FC=3cm.
故答案为:3cm.
点评 本题主要考查了切线的性质,等边三角形的性质和解直角三角形的有关知识,题目不是太难,属于基础性题目,熟记垂径定理和勾股定理是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 屈原食品公司接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只5元.为按时完成任务,该企业招收了新工人,设新工人小明第x天生产的粽子数量为n只,n与x满足如下关系式:$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}(0<x≤5)\\(5<x≤15)\end{array}$.
屈原食品公司接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只5元.为按时完成任务,该企业招收了新工人,设新工人小明第x天生产的粽子数量为n只,n与x满足如下关系式:$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}(0<x≤5)\\(5<x≤15)\end{array}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com