
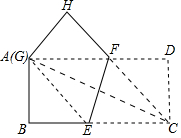
 将矩形纸片ABCD(AD>AB)折叠,使点C折叠后的对应点G恰好与A点重合,且折痕分别与边BC、AD相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边BC、AD相交于点E、F.
将矩形纸片ABCD(AD>AB)折叠,使点C折叠后的对应点G恰好与A点重合,且折痕分别与边BC、AD相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边BC、AD相交于点E、F.分析 (1)由翻折可知EC=AE,求出AE即可解决问题.
(2)结论:四边形CEGF是菱形.首先证明GF=GE,再证明四边形CEGF是平行四边形即可.
解答 解:(1)∵四边形ABCD是平行四边形,
∴∠B=90°,
∵AB=3,BE=4,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
由翻折可知EC=AE=5,
∴BC=BE+CE=9.
(2)结论:四边形CEGF是菱形.
理由:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GFE=∠FEC,
∵∠GEF=∠FEC,
∴∠GFE=∠FEG,
∴GF=GE,
∵图形翻折后EC与GE完全重合,
∴EC=GE,
∴GF=EC,∵GF∥EC
∴四边形CEGF是平行四边形,∵GF=GE,
∴四边形CEGF是菱形.
点评 本题考查翻折变换、矩形的性质、勾股定理、等腰三角形的判定和性质、平行四边形的判定和性质、菱形的判定和性质等知识,解题的关键是学会利用翻折不变性解决问题,属于中考常考题型.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
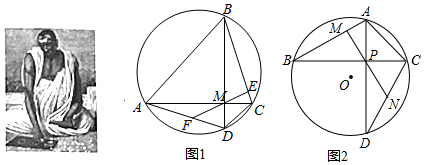
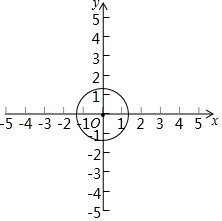 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
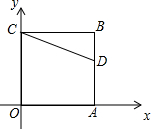 如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).
如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
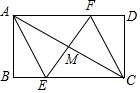 如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )| A. | AE=CF | B. | AB=AM | C. | AC⊥EF | D. | EF平分∠AEC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必然事件 | B. | 不可能发生 | C. | 可能发生 | D. | 很可能发生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com