
【题目】如图,在平面直角坐标系中,一次函数y= kx +b(k≠0)的图象分别交x轴、y轴于A、B两点,与反比例函数y=![]() (m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).
(m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).
(1)求m的值和点D的坐标;
(2)求线段AB的长度;
(3)根据图象直接写出: 当x为何值时,一次函数的值大于反比例函数的值?
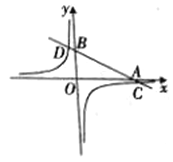
【答案】(1)m=-6,D(-2,3);(2)2![]() ;(3)<-2或0<x<6.
;(3)<-2或0<x<6.
【解析】
(1)根据函数图象上的点的坐标即可分别得出反比例函数与一次函数的解析式;把D(n,3)代入求出的反比例函数解析式即可求出点D的坐标;
(2)先求出一次函数解析式,再求点A和点B的坐标,然后用勾股定理即可求出AB得长;
(2)观察函数图象,写出符合条件时自变量x的取值范围即可.
(1)∵(6,-1)在比例函数y=![]() 的函数图象上,
的函数图象上,
∴代入后得![]() ,解得m=-6,故反比例函数解析式为y=
,解得m=-6,故反比例函数解析式为y=![]() .
.
∵D(n,3),
∴3=![]() ,
,
∴n=-2,
∴D(-2,3).
(2)设一次函数解析式为y=kx+b,把C (6,-1),D(-2,3)代入,得
![]() ,
,
解之得
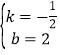 ,
,
∴![]() .
.
当x=0时,y=2;
当y=0时,x=4,
∴A(4,0),B(0,2),
∵AB=![]() ;
;
(3)根据函数图象可知,当x<-2或0<x<6时,一次函数的值大于反比例函数的值。


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙O的圆心A的坐标为(1,0),半径为1,点P为直线y=![]() x+3上的动点,过点P作⊙A的切线,且点为B,则PB的最小值是 .
x+3上的动点,过点P作⊙A的切线,且点为B,则PB的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A、C在平面直角坐标系的坐标轴上,AB=4,CB=3,点D与点A关于y轴对称,点E、F分别是线段DA、AC上的动点(点E不与A、D重合),且∠CEF=∠ACB,若△EFC为等腰三角形,则点E的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为8cm,宽为6cm的长方形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上).则剪下的等腰三角形的底边长可以是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
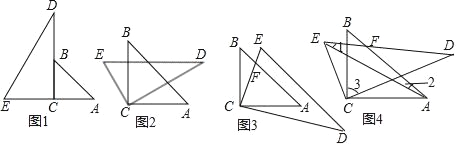
【题目】将两块三角板按图1摆放,固定三角板ABC,将三角板CDE绕点C按顺时针方向旋转,其中∠A=45°,∠D=30°,设旋转角为α,(0°<a<80°)
(1)当DE∥AC时(如图2),求α的值;
(2)当DE∥AB时(如图3).AB与CE相交于点F,求α的值;
(3)当0°<α<90°时,连结AE(如图4),直线AB与DE相交于点F,试探究∠1+∠2+∠3的大小是否改变?若不改变,请求出此定值,若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x和纵坐标y的对应值如下表,则下列说法中正确的有_______.(填序号)
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
①当x>1时,y随x的增大而减小. ②抛物线的对称轴为直线x=-![]() .
.
③当x=2时,y=-9. ④方程ax2+bx+c=0一个正数解![]() 满足1<
满足1<![]() <2.
<2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
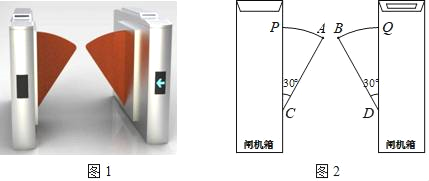
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com