
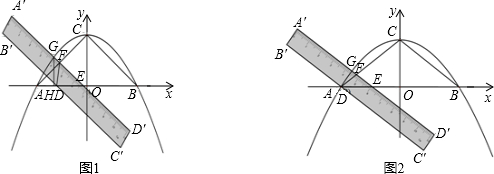
分析 (1)由y=ax2+3,得到C(0,3),OC=3×$\frac{1}{2}DE•OC=3$,求得DE=2,则S的最大值为F与C重合时,此时高最大;于是得到Smax=$\frac{1}{2}$DE•CO=3将A(-4,0)B(4,0),代入y=ax2+3即可得到结论;
(2)当D与A重合时,FD=FE,过E作EP1∥FA交B′C′于P1,则四边形P1DFE为菱形,此时F($-3,\frac{3}{4}$),由于F与P1关于x轴对称,得到P1($-3,-\frac{3}{4}$),②如图(2)若FE=ED=2时,过F作FP2∥ED交B′C′于P2,则四边形P2DEF为菱形,反向延长FP2交y轴于W,过F作FN⊥x轴于N,由于FE∥BC,∴∠FEN=∠CBO,求出sin∠FEN=sin∠CBO=$\frac{3}{5}$,在Rt△ENF中,sin∠FEN=$\frac{FN}{EF}$,即FN=$\frac{6}{5}$,解出直线AC的解析式为$y=\frac{3}{4}x+3$,即可求得P点的坐标;
(3)①设G$(x,-\frac{3}{16}x+3)$,由勾股定理即可求出结果,②在平移的过程中,QR始终平行且等于BC的一半,所以QR扫过的图形为平行四边形,如图3四边形Q1R1R2Q2为平行四边形,通过三角形相似,列比例式解得OH的长度,即可求得线段QR扫过的图形的面积和周长.
解答 (1)由y=ax2+3,得到C(0,3),OC=3×$\frac{1}{2}DE•OC=3$,求得DE=2,则S的最大值为F与C重合时,此时高最大;于是得到Smax=$\frac{1}{2}$DE•CO=3将A(-4,0)B(4,0),代入y=ax2+3即可得到结论;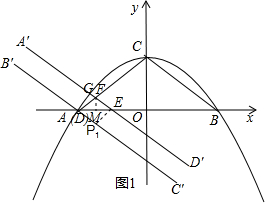 解:(1)∵y=ax2+3,∴C(0,3),即:OC=3×$\frac{1}{2}DE•OC=3$,
解:(1)∵y=ax2+3,∴C(0,3),即:OC=3×$\frac{1}{2}DE•OC=3$,
∴DE=2,
则S的最大值为F与C重合时,此时高最大;
即Smax=$\frac{1}{2}$DE•CO=3,
将A(-4,0)B(4,0),
代入y=ax2+3得:$a=-\frac{3}{16}$即$y=-\frac{3}{16}{x^2}+3$,
(2)①如图1,当D与A重合时,FD=FE,过E作EP1∥FA交B′C′于P1,
则四边形P1DFE为菱形,此时F($-3,\frac{3}{4}$),
∵F与P1关于x轴对称,
∴P1($-3,-\frac{3}{4}$),
②如图(2)若FE=ED=2时,过F作FP2∥ED交B′C′于P2,则四边形P2DEF为菱形,
反向延长FP2交y轴于W,过F作FN⊥x轴于N,
∵FE∥BC,∴∠FEN=∠CBO,
∴sin∠FEN=sin∠CBO=$\frac{3}{5}$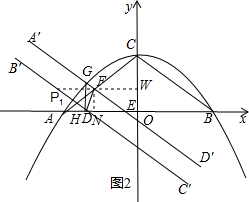 ,
,
在Rt△ENF中,sin∠FEN=$\frac{FN}{EF}$,即FN=$\frac{6}{5}$,
直线AC的解析式为$y=\frac{3}{4}x+3$,
令$y=\frac{6}{5}$,则$x=-\frac{12}{5}$,
∴FW=$\frac{12}{5}$,
∴${P_2}W=\frac{12}{5}+2=\frac{22}{5}$,
∴${P_2}(-\frac{22}{5},\frac{6}{5})$,
(3)①设G(x,-$\frac{3}{16}$x2+3),
∴$GH+HO=-x+(-\frac{3}{16}{x^2}+3)=-\frac{3}{16}{x^2}-x+3=-\frac{3}{16}{(x+\frac{8}{3})^2}+\frac{13}{3}$,
∴GH+HO的最大值为$\frac{13}{3}$,
②在平移的过程中,QR始终平行且等于BC的一半,所以QR扫过的图形为平行四边形,
如图3四边形Q1R1R2Q2为平行四边形,
设HO=m,则GH=$-\frac{3}{16}{m^2}+3$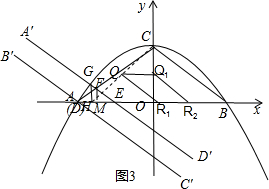 ,
,
∵△EFM∽△EGH,
∴$\frac{FM}{GH}=\frac{EM}{EH}即\frac{{\frac{3}{4}}}{{-\frac{3}{16}{m^2}+3}}=\frac{1}{m-2}$,
∴${m_1}=2\sqrt{7}-2,{m_2}=-2\sqrt{7}-2$,
即:HO=$2\sqrt{7}-2$
∵HB=HO+OB=$2\sqrt{7}-2$+4=$2\sqrt{7}+2$,
∴$H{R_1}=\frac{1}{2}HB=\sqrt{7}+1$,
∵$H{R_2}=HB-{R_2}B=2\sqrt{7}+2-2=2\sqrt{7}$,
∴R1R2=HR2-HR1=$\sqrt{7}-1$,
∴S平行四边形=($\sqrt{7}$-1)×$\frac{3}{2}$=$\frac{3}{2}$$\sqrt{7}$-$\frac{3}{3}$,
平行四边形R1R2Q2Q1的周长=$2\sqrt{7}+3$.
点评 本题考查了一次函数,二次函数,轴对称的性质,菱形的性质,相似三角形的判定和性质性质,平行四边形的面积和周长的求法,正确的画出图形是解题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
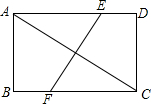 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C和点A重合,则折痕EF的长为( )
如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C和点A重合,则折痕EF的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{8}$ | C. | 15 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com