
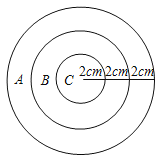
【题目】如图为一个封闭的圆形装置,整个装置内部为A、B、C三个区域(A、B两区域为圆环,C区域为小圆),具体数据如图.
(1)求出A、B、C三个区域三个区域的面积:SA= ,SB= ,SC= ;
(2)随机往装置内扔一粒豆子,多次重复试验,豆子落在B区域的概率PB为多少?
(3)随机往装置内扔180粒豆子,请问大约有多少粒豆子落在A区域?
科目:初中数学 来源: 题型:
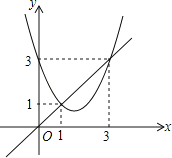
【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①bc>0;②b2﹣4c>0;③b+c+1=0;④3b+c+6=0;⑤当1<x<3时,x2+(b﹣1)x+c<0.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国诗词大会》以“赏中华诗词,寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱,某中学为了解学校学生的诗词水平,从八、九年级各随机抽取了20名学生进行了测试,并将八、九年级测试成绩(百分制,单位:分)整理如下:
收集数据
八年级 93 92 84 55 85 82 66 74 88 67 87 87 67 61 87 61 78 57 72 75
九年级 68 66 79 92 86 87 61 86 90 83 90 78 70 67 53 79 86 71 61 89
整理数据按如下分数段整理数据,并补全表格:
测试成绩x(分) | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
八 | 2 | 4 | |||
九 | 1 | 5 | 5 | 6 | 3 |
说明:测试成绩x(分),其中x≥80为优秀,70≤x<80为良好,60≤x<70为合格,0≤x<60为不合格)
分析数据补全下列表格中的统计量:
年级 | 平均数 | 中位数 | 众数 |
八 | 75.9 | 76.5 | |
九 | 77.1 | 79 | 86 |
得出结论
(1)在此次测试中,有位同学的成绩是78span>分,在他所在的年级属于中等偏上,则这位同学属于哪个年级?
(2)若九年级有800名学生,估计九年级诗词水平达到优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的两个交点分别为
轴的两个交点分别为![]() ,
,![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
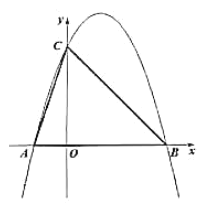
(1)求抛物线的表达式;
(2)联结![]() 、
、![]() ,求
,求![]() 的正切值;
的正切值;
(3)点![]() 在抛物线上,且
在抛物线上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=mx2﹣nx﹣m+n(m>0).
(Ⅰ)求证:该函数图象与x轴必有交点;
(Ⅱ)若m﹣n=3,
(ⅰ)当﹣m≤x<1时,二次函数的最大值小于0,求m的取值范围;
(ⅱ)点A(p,q)为函数y2=|mx2﹣nx﹣m+n|图象上的动点,当﹣4<p<﹣1时,点A在直线y=﹣x+4的上方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件![]() 元的价格购进一种商品,试销中发现这种商品每天的销售量
元的价格购进一种商品,试销中发现这种商品每天的销售量![]() (件)与每件的销售价
(件)与每件的销售价![]() (元)满足一次函数关系
(元)满足一次函数关系![]() .
.
(1)求商场销售这种商品每天的销售利润![]() (元)与每件销售价
(元)与每件销售价![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(2)商场每天销售这种商品的销售利润能否达到![]() 元?如果能,求出此时的销售价格;如果不能,说明理由.
元?如果能,求出此时的销售价格;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
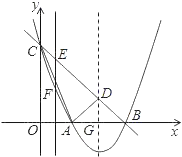
【题目】如图,顶点坐标为(2,﹣1)的抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的表达式;
(2)设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
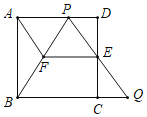
【题目】如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:![]() ;
;
(2)过点E作![]() 交PB于点F,连结AF,当
交PB于点F,连结AF,当![]() 时,①求证:四边形AFEP是平行四边形;
时,①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.
(1)如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
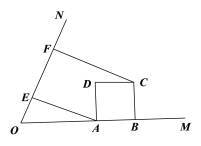
图(1)
(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
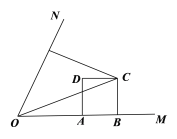
图(2)
(3)如图(3),当△AFD与△CDF相似时,求m的值.
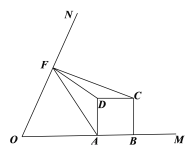
图(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com