
 上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k值为 ( )
上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k值为 ( )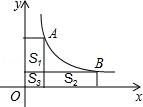
科目:初中数学 来源:不详 题型:填空题
 (x<0)的图象于B,交函数
(x<0)的图象于B,交函数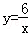 (x>0)的图象于C,则线段AB与线段AC的长度之比为 _________ .
(x>0)的图象于C,则线段AB与线段AC的长度之比为 _________ .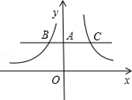
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
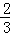 代入反比例函数y=﹣
代入反比例函数y=﹣ 中,所得函数值记为y1,又将x=y1+1代入函数中,所得函数值记为y2,再将x=y2+1代入函数中,所得函数值记为y3,…,如此继续下去.
中,所得函数值记为y1,又将x=y1+1代入函数中,所得函数值记为y2,再将x=y2+1代入函数中,所得函数值记为y3,…,如此继续下去.| y1 | y2 | y3 | y4 | y5 |
 | | | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.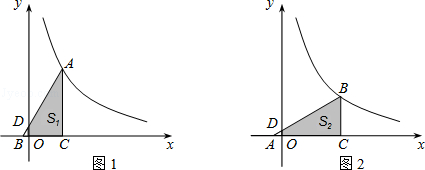
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 和
和 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
| A.3 | B.4 | C. | D.5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 上,点B在双曲线y=
上,点B在双曲线y= (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )
(k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )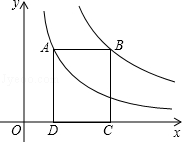
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与直线
与直线 交于A,B两点,点A在第一象限.试解答下列问题:
交于A,B两点,点A在第一象限.试解答下列问题: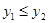 ;
;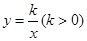 于P,Q两点,点P在第一象限, 如图2所示.
于P,Q两点,点P在第一象限, 如图2所示.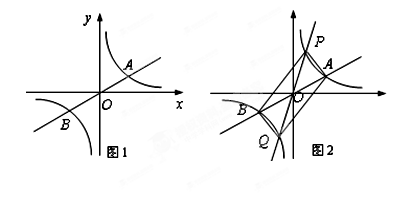
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com