
【题目】如图,在△ABC中,D是边BC上一点,若AB=10,BD=6,AD=8,AC=17,求BC的长. 
【答案】解:在△ABD中,AB=10,BD=6,AD=8,
∴AB2=BD2+AD2,
∴△ABD为直角三角形,
∴AD⊥BC,即∠ADC=90°,
在Rt△ADC中,AD=8,AC=17,
根据勾股定理得:DC= ![]() =15,
=15,
∴BC=BD+CD=6+15=21
【解析】在三角形ABD中,利用勾股定理的逆定理判断得到△ABD为直角三角形,即AD垂直于BC,在直角三角形ADC中,利用勾股定理求出DC的长,由BD+DC求出BC的长.
【考点精析】本题主要考查了勾股定理的概念和勾股定理的逆定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计黄冈市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在1000个数据中,用适当的方法抽取50个体为样本进行统计,频数分布表中54.5~57.5这一组的频率为0.12,估计总体数据落在54.5~57.5之间的约有( )个.
A.120B.60C.12D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与-1表示的点重合,则-7表示的点与数__________表示的点重合;
(2)若-1表示的点与8表示的点重合,回答以下问题:
① 12表示的点与数___________表示的点重合;
![]()
② 若数轴上A、B两点之间的距离为2017(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x﹣4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
x﹣4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )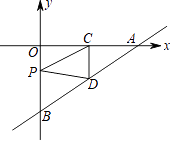
A.(0,﹣1)
B.(0,﹣2)
C.(0,﹣3)
D.(0,﹣4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com