
 如图,E在矩形ABCD的AD边上,AE=3,ED=5,DC=10,F,H分别在AB,CD上,四边形EFGH是菱形,则△FBG的面积S的取值范围是( )
如图,E在矩形ABCD的AD边上,AE=3,ED=5,DC=10,F,H分别在AB,CD上,四边形EFGH是菱形,则△FBG的面积S的取值范围是( )| A. | 0<S≤15 | B. | 2<S≤12 | C. | 1<S≤15 | D. | 0<S≤12 |
分析 由于四边形ABCD为矩形,四边形HEFG为菱形,易证△HDE≌△GFP,得到GP=DE=5,即无论菱形EFGH如何变化,点G到直线AB的距离始终为定值5,先求出AF的取值范围,S的面积可以表示成x的函数,根据函数的性质,就可以求出最值.
解答  解:过点G作GP⊥AB于P,连接HF,
解:过点G作GP⊥AB于P,连接HF,
在矩形ABCD中,
∵CD∥AB,
∴∠DHF=∠HFP,
∵四边形EFGH是菱形,
∴EH∥GF,
∠EHF=∠HFG,
∴∠DHE=∠HFG,
∵∠D=∠P=90°,
在△HDE与△GFP中,
$\left\{\begin{array}{l}{∠HDE=∠GFP}\\{∠D=∠P}\\{EH=FG}\end{array}\right.$,
∴△HDE≌△GFP(AAS),
∴GP=DE=5,
∴即无论菱形EFGH如何变化,点G到直线AB的距离始终为定值5,
∴S△GFB=$\frac{1}{2}$×5•BF,
当BF=0时,S=0,
当BF最大时,AF最小,
设DH=x,则EH2=25+x2,
∴EF2=25+x2,
∴AF2=25-x2-9=x2+16,
∴当AF=4时,BF=6,
∴S最大=$\frac{1}{2}×5×6$=15,
∴△FBG的面积S的取值范围是:0<S≤15,
故选A.
点评 本题考查了矩形的性质,菱形的性质,全等三角形的判定与性质,勾股定理.解题的关键是作辅助线:过F作FM⊥DC,交DC延长线于M,连接GE,构造全等三角形和内错角.


科目:初中数学 来源: 题型:解答题

| 竖式纸盒(个) | 横式纸盒(个) | |
| x | 100-x | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,CD,CE是⊙O的两条弦,A,B分别是$\widehat{CD}$和$\widehat{CE}$的中点,连接AB交CD于点F,交CE于点H,求证:CF=CH.
如图所示,CD,CE是⊙O的两条弦,A,B分别是$\widehat{CD}$和$\widehat{CE}$的中点,连接AB交CD于点F,交CE于点H,求证:CF=CH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
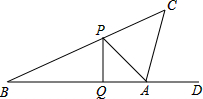 如图,小唐同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处;此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
如图,小唐同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处;此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 正方形纸片ABCD的对称中心为O,翻折∠A使顶点A重合于对角线AC上一点P,EF是折痕:
正方形纸片ABCD的对称中心为O,翻折∠A使顶点A重合于对角线AC上一点P,EF是折痕:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com