
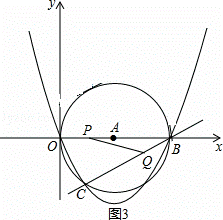
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+c(a≠0)过O、B、C三点,B、C坐标分别为(10,0)和(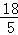 ,﹣
,﹣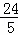 ),以OB为直径的⊙A经过C点,直线l垂直x轴于B点.
),以OB为直径的⊙A经过C点,直线l垂直x轴于B点.
(1)求直线BC的解析式;
(2)求抛物线解析式及顶点坐标;
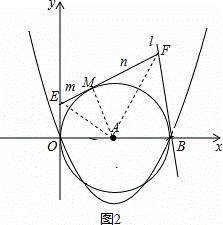
(3)点M是⊙A上一动点(不同于O,B),过点M作⊙A的切线,交y轴于点E,交直线l于点F,设线段ME长为m,MF长为n,请猜想m•n的值,并证明你的结论;
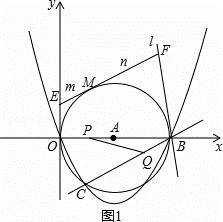
(4)若点P从O出发,以每秒一个单位的速度向点B作直线运动,点Q同时从B出发,以相同速度向点C作直线运动,经过t(0<t≤8)秒时恰好使△BPQ为等腰三角形,请求出满足条件的t值.

解:(1)设直线BC的解析式为y=kx+b,
∵直线BC经过B、C,
∴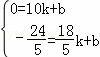 ,
,
解得: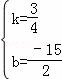 ,
,
∴直线BC的解析式为;y= x﹣
x﹣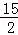 .
.
(2)∵抛物线y=ax2+bx+c(a≠0)过O、B、C三点,B、C坐标分别为(10,0)和(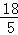 ,﹣
,﹣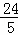 ),
),
∴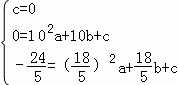 ,
,
解得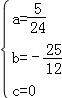 ,
,
∴抛物线的解析式为:y=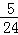 x2﹣
x2﹣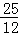 x;
x;
∴x=﹣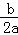 =﹣
=﹣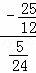 =5,y=
=5,y=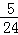 x2﹣
x2﹣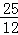 x=
x=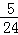 ×52﹣
×52﹣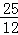 ×5=﹣
×5=﹣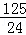 ,
,
∴顶点坐标为(5,﹣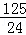 );
);
(3)m•n=25;
如图2,连接AE、AM、AF,则AM⊥EF,
在RT△AOE与RT△AME中
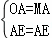
∴Rt△AOE≌RT△AME(HL),
∴∠OAE=∠MAE,
同理可证∠BAF=∠MAF,
∴∠EAF=90°,
在RT△EAF中,根据射影定理得AM2=EM•FM,
∵AM=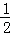 OB=5,ME=m,MF=n,
OB=5,ME=m,MF=n,
∴m•n=25;
(4)如图3.有三种情况;
①当PQ=BQ时,作QH⊥PB,
∵直线BC的斜率为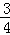 ,∴HQ:BQ=3:5,HB:BQ=4:5;
,∴HQ:BQ=3:5,HB:BQ=4:5;
∵HB=(10﹣t)×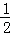 ,BQ=t,
,BQ=t,
∴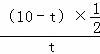 =
=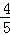 ,
,
解得;t=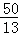 ,
,
②当PB=QB时,则10﹣t=t,
解得t=5,
③当PQ=PB时,作QH⊥OB,则PQ=PB=10﹣t,BQ=t,HP=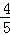 t﹣(10﹣t),QH=
t﹣(10﹣t),QH=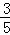 t;
t;
∵PQ2=PH2+QH2,
∴(10﹣t)2=【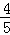 t﹣(10﹣t)]2+(
t﹣(10﹣t)]2+(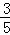 t)2;
t)2;
解得t=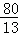 .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
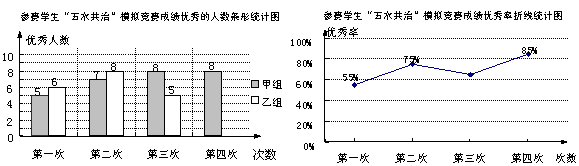
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整.
(2)已求得甲组成绩优秀人数的平均数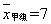 ,方差
,方差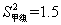 ,请通过计算说明,哪一组成绩优秀的人数较稳定?
,请通过计算说明,哪一组成绩优秀的人数较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
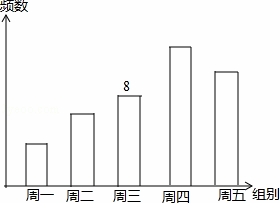
某校八年级一班进行为期5天的图案设计比赛,作品上交时限为周一至周五,班委会将参赛逐天进行统计,并绘制成如图所示的频数直方图.已知从左到右各矩形的高度比为2:3:4:6:.且已知周三组的频数是8.
(1)本次比赛共收到 40 件作品.
(2)若将各组所占百分比绘制成扇形统计图,那么第五组对应的扇形的圆心角是 90 度.
(3)本次活动共评出1个一等奖和2个二等奖,若将这三件作品进行编号并制作成背面完全相同的卡片,并随机抽出两张,请你求出抽到的作品恰好一个一等奖,一个二等奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,贤贤同学用手工纸制作 一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是( )
一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是( )

|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
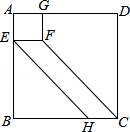
如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com