【题目】程大位是我国明朝商人，珠算发明家，他60岁时完成的《直指算法综宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法，书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁，意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人，则小和尚有__________人．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于F点，连接AD、CF．
（1）求证：四边形ADCF是平行四边形；
（2）当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在下列解答中，填写适当的理由或数学式：
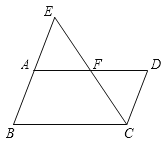
（1）∵EB∥DC， （已知）
∴∠DAE=∠__. （ ___________________________________）
（2）∵∠BCF+∠AFC=180°，（已知）
∴ ____∥___. （ ___________________________________）
（3）∵ ____∥___， （已知）
∴∠EFA=∠ECB . （ ___________________________________）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（
分）如图，管中放置着三根同样的绳子
， 
， 
．
（
）小明从
这三根绳子中随机选一根，恰好选中绳子
的概率是__________．
（
）小明先从左端
， 
， 
三个绳头中随机选两个打一个结，再从右端
， 
， 
三个绳头中随机选两个打一个结，求这三根绳子能连结成一根长绳的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
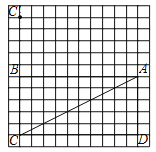
【题目】如图，12×12的正方形网格中的每个小正方形的边长都是1，正方形的顶点叫做格点．矩形ABCD的四个顶点A，B，C，D都在格点上，将△ADC绕点A顺时针方向旋转得到△AD′C′，点C与点C′为对应点．
（1）在正方形网格中确定D′的位置，并画出△AD′C′；
（2）若边AB交边C′D′于点E，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，网格中的每一个小方格都是是边长为 1 个单位的正方形，只能使用无刻度直尺，请以格点为顶点按照以下要求作图：
（1）请在图 1 中画出ABC，其中AC=
，AB=
，BC=
；
（2）请在图 2 中画出面积为 8 的正方形 ABCD，且找出点 O，使得经过点 O 的所有直线都平分正方形ABCD 的面积，保留作图痕迹．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为提高市民的环保意识，倡导“节能减排，绿色出行”，某市计划在城区投放一批“共享单车”这批单车分为A，B两种不同款型，其中A型车单价400元，B型车单价320元．
（1）今年年初，“共享单车”试点投放在某市中心城区正式启动．投放A，B两种款型的单车共100辆，总价值36800元．试问本次试点投放的A型车与B型车各多少辆？
（2）试点投放活动得到了广大市民的认可，该市决定将此项公益活动在整个城区全面铺开．按照试点投放中A，B两车型的数量比进行投放，且投资总价值不低于184万元．请问城区10万人口平均每100人至少享有A型车与B型车各多少辆？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有甲、乙两个不透明的布袋，甲袋中有2个完全相同的小球，分别标有数字0和－2；乙袋中有3个完全相同的小球，分别标有数字－2，0和1，小明从甲袋中随机取出1个小球，记录标有的数字为x，再从乙袋中随机取出1个小球，记录标有的数字为y，这样确定了点Q的坐标(x，y)．
（1）写出点Q所有可能的坐标；
（2）求点Q在x轴上的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
