
【题目】如图,AC是![]() 的直径,AB与
的直径,AB与![]() 相切于点A,四边形ABCD是平行四边形,BC交
相切于点A,四边形ABCD是平行四边形,BC交![]() 于点E.
于点E.

![]() 判断直线CD与
判断直线CD与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() 的半径为5cm,弦CE的长为8cm,求AB的长.
的半径为5cm,弦CE的长为8cm,求AB的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
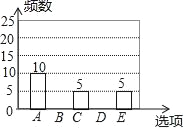
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
选项 | 频数 | 频率 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的AC的长;
,请直接写出所有满足条件的AC的长;
![]() 如图1,在四边形ABCD中,
如图1,在四边形ABCD中,![]() ,对角线BD平分
,对角线BD平分![]() ,
,![]() 求证:
求证:![]() 是比例三角形.
是比例三角形.
![]() 如图2,在
如图2,在![]() 的条件下,当
的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图2,正方形
,如图2,正方形![]() 的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈
的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落在圈
个边长,落在圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从圈
,就从圈![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落得圈
个边长,落得圈![]() ;…设游戏者从圈
;…设游戏者从圈![]() 起跳.
起跳.
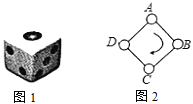
(1)小贤随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(2)小南随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小贤落回到圈
,并指出他与小贤落回到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
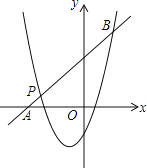
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,﹣2),B(3,4).
(1)求抛物线的表达式及对称轴;
(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,且点D纵坐标为t,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川泸州8分)如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.

(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com