
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() .
.
(1)求![]() 满足的关系式及
满足的关系式及![]() 的值;
的值;
(2)当![]() 时,求抛物线解析式,并直接写出当
时,求抛物线解析式,并直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
(3)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
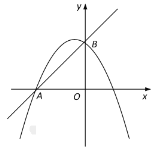
(4)如图,当![]() 时,在第二象限的抛物线上找点
时,在第二象限的抛物线上找点![]() ,使
,使![]() 的面积最大,求出点
的面积最大,求出点![]() 坐标.
坐标.
【答案】(1)b=2a+1,c=2;(2)![]() ;-2<x<3;(3)
;-2<x<3;(3)![]() ;(4)(-1,2)
;(4)(-1,2)
【解析】
(1)先求出点A和点B的坐标,然后将点A和点B的坐标代入二次函数解析式中即可求出结论;
(2)联立方程即可求出a和b的值,从而求出抛物线的解析式,然后求出抛物线的对称轴,即可求出抛物线与x轴的另一个交点坐标,最后根据图象即可求出结论;
(3)用含a的式子表示出抛物线的对称轴,然后根据抛物线对称轴两侧的增减性即可求出结论;
(4)先求出抛物线的解析式,过点P作PQ⊥x轴交AB于点Q,设点P的坐标为(x,![]() ),则点Q的坐标为(x,
),则点Q的坐标为(x,![]() ),从而求出PQ,然后利用“铅垂高,水平宽”即可求出S△PAB与x的函数关系式,然后利用二次函数求最值即可求出结论.
),从而求出PQ,然后利用“铅垂高,水平宽”即可求出S△PAB与x的函数关系式,然后利用二次函数求最值即可求出结论.
解:(1)将y=0代入![]() 中,解得:x=-2;将x=0代入
中,解得:x=-2;将x=0代入![]() 中,解得:y=2
中,解得:y=2
∴点A的坐标为(-2,0),点B的坐标为(0,2)
将点A、B的坐标代入![]() 中,得
中,得
![]()
解得:b=2a+1,c=2;
(2)∵![]()
解得: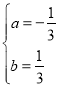
∴抛物线解析式为![]()
抛物线的对称轴为:直线x=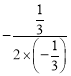 =
=![]()
∴抛物线与x轴的另一个交点坐标为![]() ×2-(-2)=3
×2-(-2)=3
由图象可知:当![]() 时,-2<x<3
时,-2<x<3
(3)抛物线的对称轴为直线x=![]() ,开口向下
,开口向下
∴x≤![]() 时,y随x的增大而增大
时,y随x的增大而增大
∵当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,
的增大而增大,
∴![]() ≥0
≥0
∴2a+1≥0
解得:a≥![]()
∴![]()
(4)当![]() 时,抛物线的解析式为
时,抛物线的解析式为![]()
过点P作PQ⊥x轴交AB于点Q
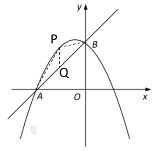
设点P的坐标为(x,![]() ),则点Q的坐标为(x,
),则点Q的坐标为(x,![]() )
)
∴PQ=(![]() )-(
)-(![]() )=
)=![]()
∴S△PAB=![]() PQ·
PQ·![]()
=![]() (
(![]() )×2
)×2
=![]()
=![]()
∴当x=-1,S△PAB最大,S△PAB最大值为1
此时点P的坐标为(-1,2)


科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,开展了“第二课堂”的活动,推出了以下四种选修课程:A.绘画;B.唱歌;C.演讲;D.十字绣.学校规定:每个学生都必须报名且 只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计, 并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
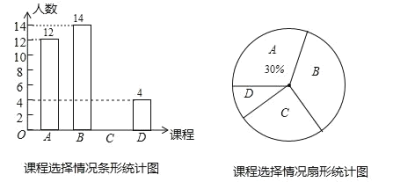
(1)这次学校抽查的学生人数是 ,C 所占圆心角为 ;
(2)将条形统计图补充完整;
(3)如果该校共有1000名学生,请你估计该校报D的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象分别位于第二、第四象限,
的图象分别位于第二、第四象限,![]() 、
、![]() 两点在该图象上,下列命题:①过点
两点在该图象上,下列命题:①过点![]() 作
作![]() 轴,
轴,![]() 为垂足,连接
为垂足,连接![]() .若
.若![]() 的面积为3,则
的面积为3,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() 其中真命题个数是( )
其中真命题个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 中点,以
中点,以![]() 为边作正方形
为边作正方形![]() ,边
,边![]() 交
交![]() 于点
于点![]() .在边
.在边![]() 上取点
上取点![]() 使
使![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
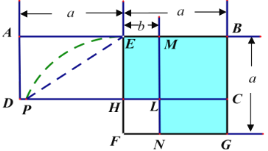
(1)请你利用该图解释平方差公式:![]() .
.
(2)现以点![]() 为圆心,
为圆心,![]() 为半径作圆弧交线段
为半径作圆弧交线段![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 在同一直线上,求
在同一直线上,求![]() 的值?
的值?
(3)记![]() 的面积为
的面积为![]() ,图中四边形
,图中四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:![]() .非常了解;
.非常了解;![]() .比较了解;
.比较了解;![]() .基本了解;
.基本了解;![]() .不了解,根据调查统计结果,绘了不完整的两种统计图表.请结合统计图表,回答下列问题:
.不了解,根据调查统计结果,绘了不完整的两种统计图表.请结合统计图表,回答下列问题:
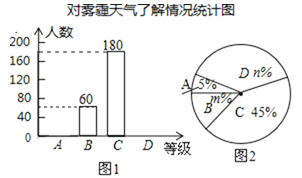
(1)本次参与调查的市民共有 人,![]() ,
,![]() ;
;
(2)统计图中扇形![]() 的圆心角是 度,并补全条形统计图;
的圆心角是 度,并补全条形统计图;
(3)某中学准备开展关于雾霾的知识竞赛,九(3)班班主任欲从2名男生和3名女生中任选2人参加比赛,求恰好选中“1男1女”的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某学校为了了解九年级学生的体能情况,抽取了部分学生进行了体能测试,学生的测试成绩分四类:A:优秀;B:良好;C:合格;D不合格,将抽测学生的成绩绘制成如下两幅不完整的统计图,请根据统计图解答下列问题:
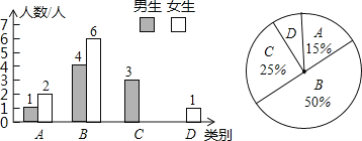
(1)求本次调查的学生总人数;
(2)成绩为C的女生有______人,成绩为D的男生有______人;
(3)扇形统计图中成绩为D的学生所对应的扇形的圆心角度数为______;
(4)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟) | 140 | 160 | 169 | 170 | 177 | 180 |
人数 | 1 | 1 | 1 | 2 | 3 | 2 |
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.方差是135B.平均数是170C.中位数是173.5D.众数是177
查看答案和解析>>
科目:初中数学 来源: 题型:
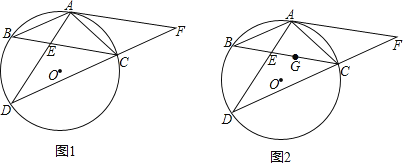
【题目】如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过点C作∠BCD=∠ACB交⊙O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:ED=EC;
(2)求证:AF是⊙O的切线;
(3)如图2,若点G是△ACD的内心,BCBE=25,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com