
【题目】请阅读下列材料:
问题:已知方程![]() ,求一元二次方程,使它的根分别是已知方程根的2倍.
,求一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为![]() ,则
,则![]() ,所以
,所以![]() .
.
把![]() 代入已知方程,得
代入已知方程,得![]()
化简,得![]()
故所求方程为![]() .
.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: .
,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: .
(2)已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
(3)已知关于![]() 的方程
的方程![]() 有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)它的根分别是已知方程根的相反数,因此所求方程的根为y,则y=-x,将x=-y代入方程就可得到所求的方程.(2)设所求方程的根为y,可得到x=![]() , 将其代入方程,就可得到a+by+cy2=0,再分情况讨论:当c=0和x≠0,即可求解.(3)设所求方程的根为y,由已知可得到y=x2 , 由此可得到x=
, 将其代入方程,就可得到a+by+cy2=0,再分情况讨论:当c=0和x≠0,即可求解.(3)设所求方程的根为y,由已知可得到y=x2 , 由此可得到x=![]() , 分别将x的值代入方程,就可得到所求的方程.
, 分别将x的值代入方程,就可得到所求的方程.
(1)设所求方程的根为![]() ,则
,则![]() ,
,
所以![]() .
.
把![]() 代入已知方程,得,
代入已知方程,得,![]() ,
,
化简,得![]() ,
,
故所求方程为![]() ;
;
(2)设所求方程的根为![]() ,则
,则![]() ,于是
,于是![]() ,
,
把![]() 代入方程
代入方程![]() ,得
,得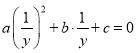 ,
,
去分母,得![]() ,
,
若![]() ,有
,有![]() ,
,
于是方程![]() 有一个根为0,不符合题意,
有一个根为0,不符合题意,
![]() ,
,
故所求方程为![]() ;
;
(3)设所求方程的根为![]() ,则
,则![]() ,
,
所以![]() ,
,
①当![]() 时,把
时,把![]() 代入已知方程,得
代入已知方程,得
![]() ,即
,即![]() ;
;
②当![]() 时,把
时,把![]() 代入已知方程,得
代入已知方程,得
![]() ,即
,即![]()
∴所求方程为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】我县“果菜大王”王大炮收货番茄20吨,青椒12吨.现计划租用甲、乙两种货车共8辆将这批果菜全部运往外地销售,已知一辆甲种货车可装番茄4吨和青椒1吨,一辆乙种货车可装番茄和青椒各2吨.
(1)王灿有几种方案安排甲、乙两种货车可一次性地将果菜运到销售地?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王大炮应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A点,D点分别在x轴、y轴上,对角线BD∥x轴,反比例函数![]() 的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
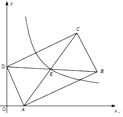
A.16B.20C.32D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:顶点、开口大小相同,开口方向相反的两个二次函数互为“反簇二次函数”.
(1)已知二次函数y=﹣(x﹣2)2+3,则它的“反簇二次函数”是__________________;
(2)已知关于x的二次函数y1=2x2﹣2mx+m+1和y2=ax2+bx+c,其中y1的图像经过点(1,1).若y1+y2与y1互为“反簇二次函数”.求函数y2的表达式,并直接写出当0≤x≤3时,y2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
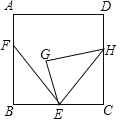
查看答案和解析>>
科目:初中数学 来源: 题型:
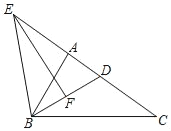
【题目】已知:如图,在△ABC中,点D在边AC上,BD的垂直平分线交CA的延长线于点E,交BD于点F,联结BE,ED2=EAEC.
(1)求证:∠EBA=∠C;
(2)如果BD=CD,求证:AB2=ADAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com