
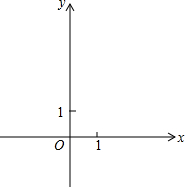 如图,在平面直角坐标系xOy中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
如图,在平面直角坐标系xOy中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.分析 (1)可求得抛物线对称轴方程和反比例函数解析式,则可求得A点坐标;
(2)可求得B点坐标,再由OC=3OB可求得C点坐标,利用待定系数法可求得直线AC的表达式;
(3)当AB为菱形的边时,则BE=AB或AE=AB,设出E点坐标,可表示出BE的长,可得到关于E点坐标的方程,可求得E点坐标,由AB∥EF,则可求得F点的坐标;当AB为对角线时,则EF被AB垂直平分,则可求得E的纵坐标,从而可求得E点坐标,利用对称性可求得F点的坐标.
解答 解:
(1)由题意可知二次函数图象的对称轴是直线x=1,反比例函数解析式是y=$\frac{5}{x}$,
把x=1代入y=$\frac{5}{x}$,得y=5,
∴点A的坐标为(1,5);
(2)由题意可得点B的坐标为(1,0),
∵OC=3OB,
∴OC=3,
∵m>0,
∴m=3,
可设直线AC的表达式是y=kx+3,
∵点A在直线AC上,
∴k=2,
∴直线AC的表达式是y=2x+3;
(3)当AB、BE为菱形的边时,如图1,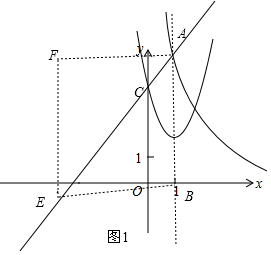
设E(x,2x+3),则BE=$\sqrt{(x-1)^{2}+(2x+3)^{2}}$,
∵四边形ABEF为菱形,
∴AB=BE=5,
∴$\sqrt{(x-1)^{2}+(2x+3)^{2}}$=5,解得x=1(E、A重合,舍去)或x=-3,
此时E(-3,-3),
∵EF∥AB且EF=AB,
∴F(-3,2),
当AB、AE为边时,则AE=AB=5,
同理可求得AE=$\sqrt{(x-1)^{2}+(2x+3-5)^{2}}$,
∴$\sqrt{(x-1)^{2}+(2x+3-5)^{2}}$=5,解得x=1-$\sqrt{5}$(此时F点在第三象限,舍去)或x=1+$\sqrt{5}$,
∴E(1+$\sqrt{5}$,5+2$\sqrt{5}$),
∵EF∥AB且EF=AB,
∴F(1+$\sqrt{5}$,2$\sqrt{5}$);
当AB为对角线时,如图2,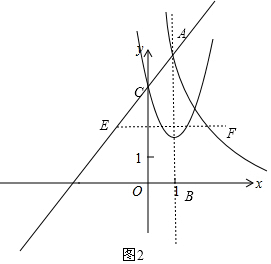
则EF过AB的中点,
∵A(1,5),B(1,0),
∴AB的中点为(1,$\frac{5}{2}$),
∵EF⊥AB,
∴EF∥x轴,
∴E点纵坐标为$\frac{5}{2}$,代入y=2x+3可得$\frac{5}{2}$=2x+3,解得x=-$\frac{1}{4}$,
∴E(-$\frac{1}{4}$,$\frac{5}{2}$),
∴F($\frac{9}{4}$,$\frac{5}{2}$);
综上可知F点的坐标为(-3,2)或(1+$\sqrt{5}$,2$\sqrt{5}$)或($\frac{9}{4}$,$\frac{5}{2}$).
点评 本题为二次函数的综合应用,涉及待定系数法、菱形的性质、勾股定理、方程思想及分类讨论思想等.在(1)中确定出A点的横坐标是解题的关键,在(2)中求得C点坐标是解题的关键,在(3)中确定出E点的位置是解题的关键,注意分情况讨论.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:选择题
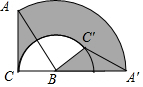 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )| A. | 4π+2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{16}{3}$π+2$\sqrt{3}$ | D. | 4π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
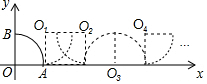 如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )
如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )| A. | (16+4π,0) | B. | (14+4π,2) | C. | (14+3π,2) | D. | (12+3π,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
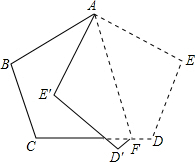 将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在E′,D′点.已知∠AFC=76°,则∠CFD′等于( )
将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在E′,D′点.已知∠AFC=76°,则∠CFD′等于( )| A. | 15° | B. | 25° | C. | 28° | D. | 31° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
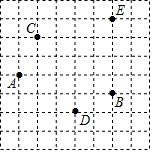 如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.
如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com