
 如图,平面直角坐标系中,直线AB:y=-x+b交y轴于点A(0,4),交x轴于点B.
如图,平面直角坐标系中,直线AB:y=-x+b交y轴于点A(0,4),交x轴于点B.分析 (1)把点A的坐标代入直线解析式可求得b=4,则直线的解析式为y=-x+4,令y=0可求得x=4,故此可求得点B的坐标;
(2)①由题l垂直平分OB可知OE=BE=2,将x=2代入直线AB的解析式可求得点D的坐标,设点P的坐标为(2,n),然后依据S△APB=S△APD+S△BPD可得到△APB的面积与n的函数关系式为S△APB=2n-4;
②由S△ABP=8得到关于n的方程可求得n的值,从而得到点P的坐标;
③如图1所示,过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.设点C的坐标为(p,q),先证明△PCM≌△CBN,得到CM=BN,PM=CN,然后由CM=BN,PM=CN列出关于p、q的方程组可求得p、q的值;如图2所示,同理可求得点C的坐标.
解答 解:(1)∵把A(0,4)代入y=-x+b得b=4
∴直线AB的函数表达式为:y=-x+4.
令y=0得:-x+4=0,解得:x=4
∴点B的坐标为(4,0).
(2)①∵l垂直平分OB,
∴OE=BE=2.
∵将x=2代入y=-x+4得:y=-2+4=2.
∴点D的坐标为(2,2).
∵点P的坐标为(2,n),
∴PD=n-2.
∵S△APB=S△APD+S△BPD,
∴S△ABP=$\frac{1}{2}$PD•OE+$\frac{1}{2}$PD•BE=$\frac{1}{2}$(n-2)×2+$\frac{1}{2}$(n-2)×2=2n-4.
②∵S△ABP=8,
∴2n-4=8,解得:n=6.
∴点P的坐标为(2,6).
③如图1所示:过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.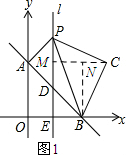
设点C(p,q).
∵△PBC为等腰直角三角形,PB为斜边,
∴PC=CB,∠PCM+∠MCB=90°.
∵CM⊥l,BN⊥CM,
∴∠PMC=∠BNC=90°,∠MPC+∠PCM=90°.
∴∠MPC=∠NCB.
在△PCM和△CBN中,
$\left\{\begin{array}{l}{∠PMC=∠BNC=90°}\\{∠MPC=∠NCB}\\{PC=BC}\end{array}\right.$,
∴△PCM≌△CBN.
∴CM=BN,PM=CN.
∴$\left\{\begin{array}{l}{p-4=6-q}\\{q=p-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{p=6}\\{q=4}\end{array}\right.$.
∴点C的坐标为(6,4).
如图2所示:过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.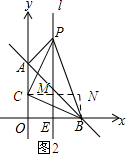
设点C(p,q).
∵△PBC为等腰直角三角形,PB为斜边,
∴PC=CB,∠PCM+∠MCB=90°.
∵CM⊥l,BN⊥CM,
∴∠PMC=∠BNC=90°,∠MPC+∠PCM=90°.
∴∠MPC=∠NCB.
在△PCM和△CBN中,
$\left\{\begin{array}{l}{∠PMC=∠BNC=90°}\\{∠MPC=∠NCB}\\{PC=BC}\end{array}\right.$,
∴△PCM≌△CBN.
∴CM=BN,PM=CN.
∴$\left\{\begin{array}{l}{4-p=6-q}\\{q=2-p}\end{array}\right.$,解得$\left\{\begin{array}{l}{p=0}\\{q=2}\end{array}\right.$.
∴点C的坐标为(0,2).
综上所述点C的坐标为(6,4)或(0,2).
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了待定系数法求一次函数的解析式、割补法求面积、三角形的面积公式,全等三角形的性质可判断,由CM=BN,PM=CN列出关于p、q的方程组是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
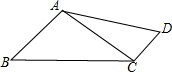 四边形ABCD中,∠B=∠D,∠BAC=120°,∠BCD=150°,若AC=5$\sqrt{3}$,AD=11,则BC的长为7$\sqrt{3}$.
四边形ABCD中,∠B=∠D,∠BAC=120°,∠BCD=150°,若AC=5$\sqrt{3}$,AD=11,则BC的长为7$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图.在边长为2的菱形ABCD中,∠A=60°,点P为射线AB上一个动点.过点P作PE⊥AB交射线AD于点E.将△AEP沿直线PE折叠,点A的对应点为F,连接FD、FC,若△FDC为直角三角形时,AP的长为$\frac{1}{2}$或$\frac{3}{2}$.
如图.在边长为2的菱形ABCD中,∠A=60°,点P为射线AB上一个动点.过点P作PE⊥AB交射线AD于点E.将△AEP沿直线PE折叠,点A的对应点为F,连接FD、FC,若△FDC为直角三角形时,AP的长为$\frac{1}{2}$或$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我市中学生视力情况 | B. | 了解一沓钞票中有没有假钞 | ||
| C. | 了解一批西瓜是否甜 | D. | 调查普宁《商城聚焦》栏目的收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com