
【题目】某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级学生参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下(单位:分):
七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分数段整理数据并补全表格:
成绩x 人数 年级 |
|
|
|
|
七年级 | 1 | 1 | 5 | 3 |
八年级 | 4 | 4 |
分析数据:补全下列表格中的统计量:
统计量 年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 93.6 | 94 | 24.2 | |
八年级 | 93.7 | 93 | 20.4 |
得出结论:你认为哪个年级学生“汉字听写”大赛的成绩比较好?并说明理由.(至少从两个不同的角度说明推断的合理性)
【答案】整理数据:八年级![]() 段1人,
段1人,![]() 段1人;分析数据:七年级众数94,八年级中位数93.5;得出结论:八年级学生大赛的成绩比较好,见解析.
段1人;分析数据:七年级众数94,八年级中位数93.5;得出结论:八年级学生大赛的成绩比较好,见解析.
【解析】
整理数据:根据八年级抽取10名学生的成绩,可得;
分析数据:根据题目给出的数据,利用众数的定义,中位数的定义求出即可;
得出结论:根据给出的平均数和方差分别进行分析,即可得出答案.
解:整理数据:八年级![]() 段1人,
段1人,![]() 段1人
段1人
分析数据,由题意,可知94分出现次数最多是4次,所以七年级10名学生的成绩众数是94,
将八年级10名学生的成绩从小到大排列为:84,88,93,93,93,94,97,98,98,99,
中间两个数分别是93,94,(93+94)÷2=93.5,
所以八年级10名学生的成绩中位数是93.5;
得出结论:认为八年级学生大赛的成绩比较好.
理由如下:八年级学生大赛成绩的平均数较高,表示八年级学生大赛的成绩较好;
八年级学生大赛成绩的方差小,表示八年级学生成绩比较集中,整体水平较好.
故答案为:整理数据:八年级![]() 段1人,
段1人,![]() 段1人;分析数据:七年级众数94,八年级中位数93.5;得出结论:八年级学生大赛的成绩比较好,见解析.
段1人;分析数据:七年级众数94,八年级中位数93.5;得出结论:八年级学生大赛的成绩比较好,见解析.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
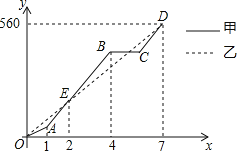
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】肥西素有“淮军故里、改革首县、花木之乡”之美誉,现就肥西以下五个旅游景点进行调查,A.“官亭林海”,B.“三河古镇”,C.“紫蓬山国家森林公园”,D.“小井庄”,E.“刘铭传故居”,为了解学生最喜欢哪一个景点(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:


(1)本次接受调查的总人数为______人,统计表中m=______,n=______.
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则景点“紫蓬山国家森林公园”、“小井庄”、“刘铭传故居”所在扇形的圆心角度数分别是__________、___________、___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:有理数![]() 用数轴上点
用数轴上点![]() 表示,
表示,![]() 叫做点
叫做点![]() 在数轴上的坐标;有理数
在数轴上的坐标;有理数![]() 用数轴上点
用数轴上点![]() 表示,
表示,![]() 叫做点
叫做点![]() 在数轴上的坐标.
在数轴上的坐标.![]() 表示数轴上的两点
表示数轴上的两点![]() ,
,![]() 之间的距离.
之间的距离.
(1)借助数轴,完成下表:
|
|
|
|
3 | 2 | 1 | 1 |
1 | 5 | ______ | ______ |
2 | -3 | ______ | ______ |
-4 | 1 | ______ | ______ |
-5 | -2 | ______ | ______ |
-3 | -6 | ______ | ______ |
(2)观察(1)中的表格内容,猜想![]() ______;(用含
______;(用含![]() ,
,![]() 的式子表示,不用说理)
的式子表示,不用说理)
(3)已知点![]() 在数轴上的坐标是-2,且
在数轴上的坐标是-2,且![]() ,利用(2)中的结论求点
,利用(2)中的结论求点![]() 在数轴上的坐标.
在数轴上的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OM上有三点A、B、C,OC=45cm, BC=15cm, AB=30cm,已知动点P、Q同时运动,其中动点P从点O出发沿OM方向以速度2cm/s匀速运动,动点Q从点C出发沿CA方向匀速运动,当点Q运动到点A时,点Q停止运动(点P继续运动).设运动时间为t秒.

(1)求点P运动到点B所用的时间;
(2)若点Q运动速度为每秒1cm,经过多少秒时,点P和点Q的距离为30cm;
(3)当PA=2PB时,点Q恰好在线段AB的三等分点的位置,求点Q的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西桂林市)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=![]() =6,∴S=
=6,∴S=![]() =
=![]() =6.
=6.
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
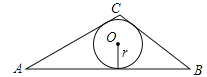
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,且AB![]() CD于点E。连接AC、OC、BC。
CD于点E。连接AC、OC、BC。
(1)求证: ![]() ACO=
ACO=![]() BCD。
BCD。
(2)若EB=![]() ,CD=
,CD=![]() ,求⊙O的直径。
,求⊙O的直径。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com