
【题目】Rt△ABC中,∠C=90°,∠B=54° ,则∠A=( )
A.36°
B.46°
C.56°
D.66°
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查方式的是( )
A. 对乌达区中学生心理健康现状的调查
B. 对冷饮市场上冰淇淋质量情况的调查
C. 审核书稿中的错别字
D. 调查乌达区中学生社会主义核心价值观的背诵情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4![]() ,∠BAC=45°.
,∠BAC=45°.
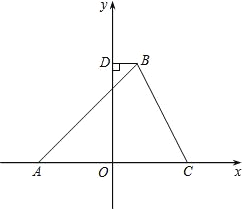
(1)求点A,C的坐标;
(2)反比例函数y=![]() 的图象经过点B,求k的值;
的图象经过点B,求k的值;
(3)在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P,O,A为顶点的三角形相似?若存在,请写出满足条件的点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市园林部门为了扩大城市的绿化面积,进行了大量的树木移栽.下表记录的是在相同的条件下移栽某种幼树的棵数与成活棵数:
移栽棵树 | 100 | 1000 | 10000 | 20000 |
成活棵树 | 89 | 910 | 9008 | 18004 |
依此估计这种幼树成活的概率约是________.(结果用小数表示,精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种面粉的质量标识为“26±0.25千克”,则下列面粉中合格的是:( )
A. 26.30千克 B. 25.70千克 C. 26.51千克 D. 25.80千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1)令P0(2,﹣3),O为坐标原点,则d(O,P0)= ;
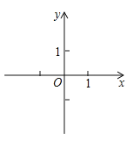
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离. 若P(a,﹣3)到直线y=x+1的直角距离为6,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com