解:由题意知方程组
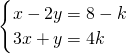
和5x-3y=0有公共解,
由x-2y=8-k变形得:k=8-x+2y,
把它代入3x+y=4k得:3x+y=4(8-x+2y),
整理得:7x-7y=32,
又∵5x-3y=0,
∴两方程联立解得:x=-

,y=-

,
把它代入k=8-x+2y得:k=-8.
故答案为:-8.
分析:由题意知方程组
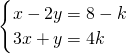
和5x-3y=0有公共解,然后用加减消元法和代入法解方程即可.
点评:本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.

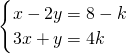 的解满足5x-3y=0?
的解满足5x-3y=0?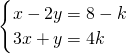 和5x-3y=0有公共解,
和5x-3y=0有公共解, ,y=-
,y=- ,
,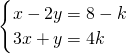 和5x-3y=0有公共解,然后用加减消元法和代入法解方程即可.
和5x-3y=0有公共解,然后用加减消元法和代入法解方程即可.
