
 ,1),B(s,t),C(
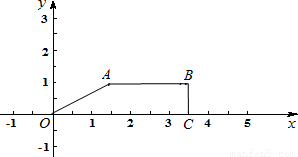
,1),B(s,t),C( ,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
 解:
解: ,1).((1分))
,1).((1分)) ,t=1.直角梯形如图所画.(2分)
,t=1.直角梯形如图所画.(2分)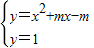 (3分)
(3分) ,不合题意,舍去.(4分)
,不合题意,舍去.(4分) ≤-m-1≤
≤-m-1≤ ,
,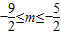 .①(5分)
.①(5分) )是直角梯形OABC的内部和其边上的一个动点,
)是直角梯形OABC的内部和其边上的一个动点, ,即-7≤m≤0. ②(6分)
,即-7≤m≤0. ②(6分) ,
, ,m(m+4)≤0,
,m(m+4)≤0,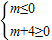 或者
或者 .(8分)
.(8分) x的下方,
x的下方,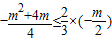 ,(10分)
,(10分)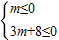 或者
或者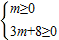 ,(*(8分)处评分后,此处不重复评分)
,(*(8分)处评分后,此处不重复评分) (11分),或m≥0 ④
(11分),或m≥0 ④ .(12分)
.(12分)

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 ,1),B(s,t),C(
,1),B(s,t),C( ,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《圆》(11)(解析版) 题型:解答题
 与
与 是否相等?请你说明理由;
是否相等?请你说明理由;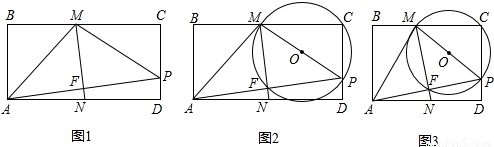
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com