
【题目】六一前夕某幼儿园园长到厂家选购A、B两种品牌的儿童服装每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍,求A、B两种品牌服装每套进价分别为多少元?
科目:初中数学 来源: 题型:
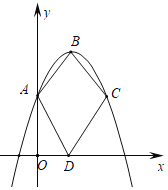
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+3x+2与y轴交于点A,点B是抛物线的顶点,点C与点A是抛物线上关于对称轴对称的两个点,点D在x轴上运动,则四边形ABCD的两条对角线的长度之和的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:在矩形ABCD中,AB=6,BC=4,点E、F分别为边AD、BC上的点,且AE=1;BF=2.
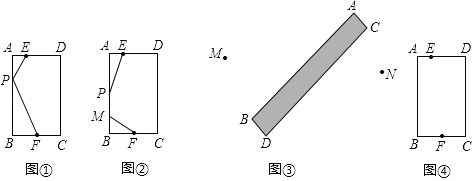
(1)如图①,P为边AB上一动点,连接EP、PF,则EP+PF的最小值为_____;
(2)如图②,P、M是AB边上两动点,且PM=2,现要求计算出EP、PM、MF和的最小值.九年级一班某兴趣小组通过讨论得出一个解决方法:在DA的延长线上取一点E',使AE'=AE,再过点E'作AB的平行线E'C,在E'C上E”的下方取点M,使E'M'=2,连接M'F,则与AB边的交点即为M,再在边AB上点M的上方取P点,且PM=2,此时EP+PM+MF的值最小.但他们不确定此方法是否可行,便去请教数学田老师,田老师高兴地说:“你们的做法是有道理的”.现在请你根据叙述作出草图并计算出EP+PM+MF的最小值;
问题解决:(3)聪聪的爸爸是供电公司的线路设计师,公司准备架设一条经过农田区的输电线路,为M、N两个村同时输电.如图所示,农田区两侧AB与CD平行,且农田区宽为0.5千米,M村到AB的距离为2千米,N村到CD的距离为1千米,M、N所在的直线与AB所夹锐角恰好为45°,根据架线要求,在农田区内的线路要与AB垂直.请你帮助聪聪的爸爸设计出最短的线路图,并计算出最短线路的长度.(要求:写出计算过程,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,抽查了一部分考生的体育测试成绩,甲、乙、丙三位同学将抽查出的学生的测试成绩按A(优秀)、B(良好)、C(及格)、D(不及格)四个等级进行统计,并将统计结果绘制成如下统计图(如图).甲同学计算出成绩为C的频率是0.2,乙同学计算出成绩为A、B、C的频率之和为0.96,丙同学计算出成绩为A的频数与成绩为C的频数之比为6:5.结合统计图回答下列问题:
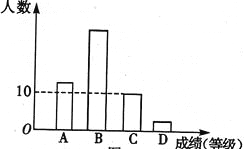
(1)这次抽查了多少人?
(2)所抽查学生体育测试成绩的中位数在哪个等级内?
(3)若该校九年级学生共有720人,请你估计这次体育测试成绩为优秀的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的现在的售价为每件55元,每星期可卖出200件,如果每件商品的售价每上涨1元,则每星期少卖10件.已知商品进价为每件50元,进行涨价销售,每件售价是整数元,且不能高于70元.
(1)每件商品的售价定为多少元时,每星期可获得利润最大?最大利润是多少元?
(2)若在销售过程中每一件商品有m(m>1)元的其他费用,商家发现当售价每件不低于65元时,每星期的销售利润随定价的增大而减小,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
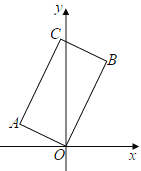
【题目】如图,在矩形AOBC中,点A的坐标为(-2,1),点C的纵坐标是4,则B,C两点的坐标分别是( )
A. (![]() ,
,![]() ),(
),(![]() ,
,![]() )B. (
)B. (![]() ,
,![]() ),(
),(![]() ,
,![]() )
)
C. (![]() ,
,![]() ),(
),(![]() ,
,![]() )D. (
)D. (![]() ,
,![]() ),(
),(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的布袋中装有1个红球,2个白球,它们除颜色外其余完全相同.
(1)从袋中任意摸出两个球,试用树状图或表格列出所有等可能的结果,并求摸出的球恰好是两个白球的概率;
(2)若在布袋中再添加a个白球,充分搅匀,从中摸出一个球,使摸到红球的概率为![]() ,试求a的值.
,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中线段AB的两个端点分别在坐标轴上,点A的坐标为(1,0),将线段AB绕点A顺时针旋转90°后,点B恰好落在反比例函数y=![]() 在第一象限内的分支上的点B′,则点B的坐标为( )
在第一象限内的分支上的点B′,则点B的坐标为( )
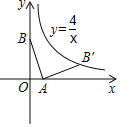
A.(0,2)B.(0,3)C.(0,4)D.(0,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小腾遇到这样一个问题:如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上.
上.![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的长.
的长.
小腾发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).

发现:![]() 的度数为 ,
的度数为 ,![]() 的长为
的长为
探究:参考小腾思考问题的方法,解决问题:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,求
,求![]() ,
,![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com