如下图，四边形OABC为直角梯形，A(4，0)，B(3，4)，C(0，4)．点M从O出发以每秒2个单位长度的速度向A运动；点N从B同时出发，以每秒1个单位长度的速度向C运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP垂直x轴于点P，连结AC交NP于Q，连结MQ．
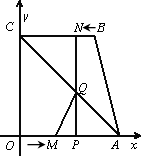
(1)谁能先到达终点________(填M或N)；
(2)求△AQM的面积S与运动时间t的函数关系式，并写出自变量t的取值范围，当t为何值时，S的值最大；
(3)是否存在点M，使得△AQM为直角三角形？若存在，求出点M的坐标，若不存在，说明理由．
科目：初中数学 来源： 题型：013
(2005·山东威海)如下图，在图(1)中，Rt△OAB绕其直角顶点O每次旋转90°，旋转三次得到右边的图形，在图(2)中，四边形OABC绕O点每次旋转120°，旋转两次得到右边的图形．
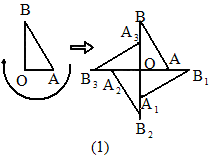
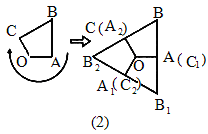
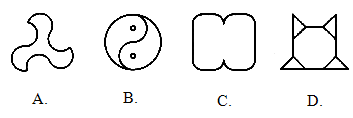
下面选项中不能通过上述方式得到的是
[ ]
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，直线AB交x轴于点A(2，0)，交抛物线
于点B(1，
)，点C到△OAB各顶点的距离相等，直线AC交y轴于点D．当x > 0时，在直线OC和抛物线上是否分别存在点P和点Q，使四边形DOPQ为特殊的梯形？若存在，求点P、Q的坐标；若不存在，说明理由．
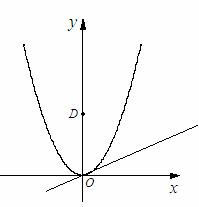
附加题：在上题中，抛物线的解析式和点D的坐标不变(如下图)．当x > 0时，在直线
(0 < k < 1)和这条抛物线上，是否分别存在点P和点Q，使四边形DOPQ为以OD为底的等腰梯形．若存在，求点P、Q的坐标；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
