
【题目】问题情境
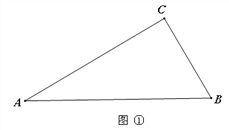
学习完本册第二章“轴对称图形”后,张老师在课堂上提出这样的问题:“如图①,在△ABC中,∠A=30°,∠B=60°,如何画一条线段把△ABC分割成两个等腰三角形?”请在图中画出这条线段,并标出相关的度数.
问题探究
探究一:课后,小华经过探究发现:如图②,在△ABC中,∠A=26°,∠B=52°,也可以画一条线段把△ABC分割成两个等腰三角形.请在图中画出这条线段,并标出相关的度数.
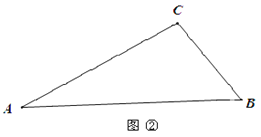
探究二:如图③,在△ABC中,当,∠B=2∠A时,是否一定存在一条线段把△ABC分割成两个等腰三角形?若能,请在图中画出这条线段,若不能,直接写出∠A的取值范围.
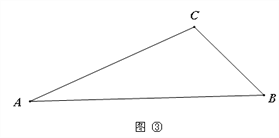
【答案】见解析
【解析】试题分析:本题考查等腰三角形的构造方法,根据垂直平分线上的点到线段两端点距离相等,则以线段AC为底,作线段AC的垂直平分线交线段AB于一点D,连接DC,则△ADC是等腰三角形,再根据三角形的外角性质可知∠CDB=2∠A,然后再根据等角对等边来判定是否为等腰三角形.
以线段AC为底,作线段AC的垂直平分线交线段AB于一点D,连接DC,则△ADC是等腰三角形,再根据三角形的外角性质可知∠CDB=2∠A=60°,
因为∠B=60°,所以∠CDB=∠B,所以△BDC是等腰三角形.
以线段AC为底,作线段AC的垂直平分线交线段AB于一点D,连接DC,则△ADC是等腰三角形,再根据三角形的外角性质可知∠CDB=2∠A=52°,
因为∠B=52°,所以∠CDB=∠B,所以△BDC是等腰三角形.
以线段AC为底,作线段AC的垂直平分线交线段AB于一点D,连接DC,则△ADC是等腰三角形,再根据三角形的外角性质可知∠CDB=2∠A= ![]() ,
,
根据等腰三角形的性质和三角形内角和性质得, ![]() ,
, ![]() ,所以
,所以![]() ,
,
所以当![]() 时,通过作线段AC的垂直平分线交线段AB于一点D,连接DC,可将
时,通过作线段AC的垂直平分线交线段AB于一点D,连接DC,可将
△ABC分为两个等腰三角形.
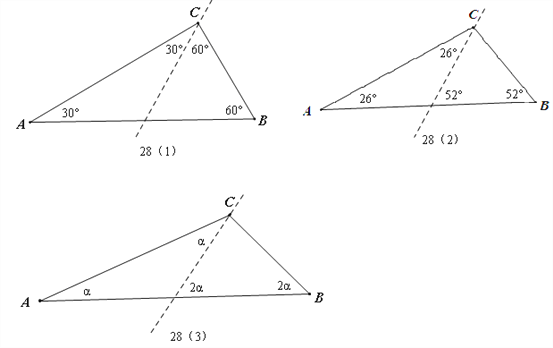
探究一:如图28(2)
探究二:设∠A=α则,∠B=2α如图28(3),0°<∠A<45°


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
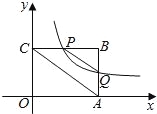
【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线![]() (x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(1)若P为边BC的中点,求双曲线的函数表达式及点Q的坐标;
(2)求k的取值范围;
(3)连接PQ,AC,判断:PQ∥AC是否总成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组量中,不是互为相反意义的量的是( ).
A.收入200元与支出20元
B.上升10米与下降7米
C.超过0.05米与不足0.03米
D.增大2岁与减少2升
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com