
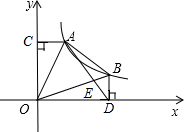
 如图,Rt△OAB中,∠OAB=90°,OA=OB,双曲线y=$\frac{k}{x}$(k>0,x>0).经过A、B两点(A在B的左侧),AC⊥y轴于C,BD⊥x轴于D,连接AD交OB于E.下列结论正确的个数是( )
如图,Rt△OAB中,∠OAB=90°,OA=OB,双曲线y=$\frac{k}{x}$(k>0,x>0).经过A、B两点(A在B的左侧),AC⊥y轴于C,BD⊥x轴于D,连接AD交OB于E.下列结论正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 延长CA、DB交于点F,则四边形OCFD是矩形,得出∠F=90°,OC=DF,得出∠1+∠2=90°,由角的互余关系得出∠2=∠3,由AAS证明△ABF≌△OAC,得出对应边相等BF=AC,AF=OC,即可得出①正确;
设AC=a,OC=b,则BF=AC=a,AF=OC=b,BD=b-a,OD=CF=a+b,由△OAC的面积=△OBD的面积=$\frac{k}{2}$,得出AC•OC=OD•BD,即a2=b2-ab,得出AC2=OC•BD,②正确;
由OD2-BD2=(a+b)2-(b-a)2=4ab=4k,得出③正确;
证出BF2=DF•BD,得出B是DF的黄金分割点,BF是较长线段,得出BF=$\frac{\sqrt{5}-1}{2}DF=\frac{\sqrt{5}-1}{2}OC$,证出$\frac{OC-BD}{OC}$=$\frac{\sqrt{5}-1}{2}$,④正确;
作EM⊥OD于M,则∠EMD=90°,EM∥BD,证明A、O、B、D四点共圆,由圆周角定理得出∠ADO=∠ABO=45°,得出△DEM是等腰直角三角形,得出EM=DM,DE=$\sqrt{2}$EM,设EM=DM=y,则OM=OD-DM=a+b-y,证出△OEM∽△ODB,得出对应边成比例得出EM=y=$\frac{a}{2}$,得出DE=$\frac{\sqrt{2}}{2}$a,由平方差公式得出AE2-DE2=2a2,即可得出结论.
解答 解:延长CA、DB交于点F,如图1所示:
则四边形OCFD是矩形,
∴∠F=90°,OC=DF,
∴∠1+∠2=90°,
∵∠AOB=90°,OA=AB,
∴∠ABO=45°,∠1+∠3=90°,
∴∠2=∠3,
在△ABF和△OAC中,$\left\{\begin{array}{l}{∠F=∠ACO=90°}&{\;}\\{∠2=∠3}&{\;}\\{AB=OA}&{\;}\end{array}\right.$,
∴△ABF≌△OAC(AAS),
∴BF=AC,AF=OC,
∴AC+BD=BF+BD=DF=OC,
即①正确;
设AC=a,OC=b,则BF=AC=a,AF=OC=b,
∴BD=b-a,OD=CF=a+b,
∵双曲线y=$\frac{k}{x}$(k>0,x>0)经过A、B两点,
∴△OAC的面积=△OBD的面积=$\frac{k}{2}$,
即$\frac{1}{2}$AC•OC=$\frac{1}{2}$OD•BD,k=ab,
∴AC•OC=OD•BD,
即ab=(a+b)(b-a),
∴a2=b2-ab,
即a2=b(b-a),
∴AC2=OC•BD,
∴②正确;
∵OD2-BD2=(a+b)2-(b-a)2=4ab=4k,
∴③正确;
∵AC=BF,DF=OC,AC2=OC•BD,
∴BF2=DF•BD,
∴B是DF的黄金分割点,BF是较长线段,
∴BF=$\frac{\sqrt{5}-1}{2}DF=\frac{\sqrt{5}-1}{2}OC$,
∵BF=DF-BD=OC-BD,
∴$\frac{OC-BD}{OC}$=$\frac{\sqrt{5}-1}{2}$,
∴④正确;
作EM⊥OD于M,如图2所示: 则∠EMD=90°,EM∥BD,
则∠EMD=90°,EM∥BD,
∵∠OAB+∠ODB=180°,
∴A、O、B、D四点共圆,
∴∠ADO=∠ABO=45°,
∴△DEM是等腰直角三角形,
∴EM=DM,DE=$\sqrt{2}$EM,
设EM=DM=y,则OM=OD-DM=a+b-y,
∵EM∥BD,
∴△OEM∽△ODB,
∴$\frac{EM}{BD}=\frac{OM}{OD}$,
即$\frac{y}{b-a}=\frac{a+b-y}{a+b}$,
解得:EM=y=$\frac{{b}^{2}-{a}^{2}}{2b}$=$\frac{ab}{2b}$=$\frac{a}{2}$,
∴DE=$\frac{\sqrt{2}}{2}$a,
∴AE2-DE2=(AE+DE)(AE-DE)=AD(AD-2DE)=$\sqrt{2}$b($\sqrt{2}$b-$\sqrt{2}$a)=2b2-2ab=2b2-2(b2-a2)=2a2,
∴⑤正确;
正确的个数有5个,
故选:D.
点评 本题是反比例函数综合题目,考查了全等三角形的判定与性质、反比例函数的运用、矩形的判定与性质、黄金分割、等腰直角三角形的判定与性质、相似三角形的判定与性质等知识;本题综合性强,难度较大,特别是⑤,需要证明四点共圆,运用圆周角定理和三角形相似才能得出结果.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com