
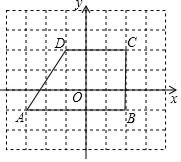
【题目】在直角坐标平面里,梯形ABCD各顶点的位置如图所示,图中每个小正方形方格的边长为1个单位长度.
(1)求梯形ABCD的面积;
(2)如果把梯形ABCD在坐标平面里先向右平移1个单位,然后向下平移2个单位得到梯形A1B1C1D1,求新顶点A1,B1,C1,D1的坐标.
【答案】(1)12 (2)A1(﹣2,﹣3),B1(3,﹣3),C1(3,0),D1(0,0)
【解析】试题分析:(1)判断出A、B、C、D四点坐标,利用梯形的面积公式计算即可;
(2)则平移公式为:![]() ,即可解决问题;
,即可解决问题;
试题解析:
(1)由图可知:
A(﹣3,﹣1)、B(2,﹣1)、C(2,2)、D(﹣1,2)
AB∥CD,BC⊥AB,
所以,梯形ABCD是直角梯形,
AB=5,DC=3,BC=3,
梯形ABCD的面积是S=![]()
(2)如果把梯形ABCD在坐标平面里先向右平移1个单位,然后向下平移2个单位,则平移公式为:![]()
所以,平移以后所得梯形A1B1C1D1各顶点的坐标分别为:
A1(﹣2,﹣3),B1(3,﹣3),C1(3,0),D1(0,0)
A1(-2,-3),B1(3,-3),C1(3,0),D1(0,0)


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在旧城改造中,要拆除一建筑物AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区.现在从离点B 24 m远的建筑物CD的顶端C测得点A的仰角为45°,点B的俯角为30°,问离点B 35 m处的一保护文物是否在危险区内?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据宁波市统计局年报,去年我市人均生产总值为104485元,104485元用科学记数法表示为( )
A.1.04485×106元
B.0.104485×106元
C.1.04485×105元
D.10.4485×104元
查看答案和解析>>
科目:初中数学 来源: 题型:
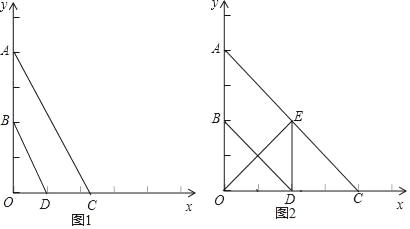
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(![]() 2,3),B(5,0),C(
2,3),B(5,0),C(![]() ,
, ![]() 2).
2).
①当![]() 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(![]() ,
, ![]() ),其中点E是函数
),其中点E是函数![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
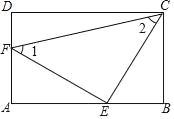
【题目】如图:在矩形ABCD中,E、F分别是AB、AD边上的点,且BE=AF,∠1=∠2.
(1)Rt△AEF与Rt△BCE全等吗?说明理由;
(2)△CEF是不是直角三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com