
 需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)
需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗) ,
, ,
, ,
,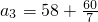 ,
, ,
, ,
, ,
, ,a8=58+30,
,a8=58+30, ,
, ,
, ,
, ,
,
 ,
, ,
, .
. ,a7+a8<a8+a8=88×2<210.
,a7+a8<a8+a8=88×2<210.
 (50+x)cm,
(50+x)cm, [
[ (50+x)+x]cm,
(50+x)+x]cm, {
{ [
[ (50+x)+x]+x}=80,
(50+x)+x]+x}=80, ,
, cm,
cm,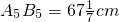 ,
, ,
, ,
, ,
, .
.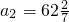 ,
, ,
, ,
, ,
,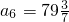 ,
,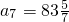 ,a8=88.
,a8=88. ,a7+a8<a8+a8=88×2<210.
,a7+a8<a8+a8=88×2<210.

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
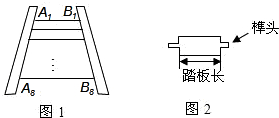 需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)
需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)查看答案和解析>>
科目:初中数学 来源: 题型:
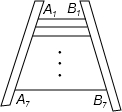 王大伯要做一张如图所示的梯子,梯子共有7级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度A1B1=0.5m,最下面一级踏板的长度A7B7=0.8m.则A3B3踏板的长度为( )
王大伯要做一张如图所示的梯子,梯子共有7级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度A1B1=0.5m,最下面一级踏板的长度A7B7=0.8m.则A3B3踏板的长度为( )| A、0.6m | B、0.65m | C、0.7m | D、0.75m |
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:解答题
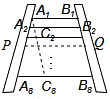
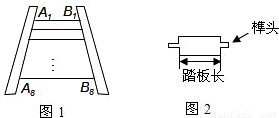
王大伯要做一张如图1的梯子,梯子共有8级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度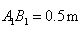 ,最下面一级踏板的长度
,最下面一级踏板的长度 .木工师傅在制作这些踏板时,截取的木板要比踏板长,以保证在每级踏板的两个外端各做出一个长为4cm的榫头(如图2所示),以此来固定踏板.现市场上有长度为2.1m的木板可以用来制作梯子的踏板(木板的宽厚和厚度正好符合要制作梯子踏板的要求),请问:制作这些踏板,王大伯最少需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)
.木工师傅在制作这些踏板时,截取的木板要比踏板长,以保证在每级踏板的两个外端各做出一个长为4cm的榫头(如图2所示),以此来固定踏板.现市场上有长度为2.1m的木板可以用来制作梯子的踏板(木板的宽厚和厚度正好符合要制作梯子踏板的要求),请问:制作这些踏板,王大伯最少需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)

查看答案和解析>>
科目:初中数学 来源:第19章《相似形》中考题集(22):19.7 应用举例(解析版) 题型:解答题
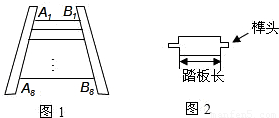
查看答案和解析>>
科目:初中数学 来源:2007年江苏省无锡市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com