
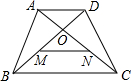
 如图,ABCD是等腰梯形,对角线AC与BD交于O点,AD=2,M、N分别是OB、OC的中点,AN与DM互相平分,则BC等于( )
如图,ABCD是等腰梯形,对角线AC与BD交于O点,AD=2,M、N分别是OB、OC的中点,AN与DM互相平分,则BC等于( )科目:初中数学 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
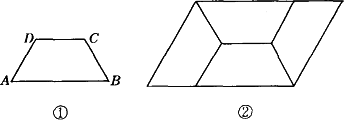
如图①四边形ABCD是等腰梯形,AB∥DC.由4个这样的等腰梯形可以拼出图②所示的平行四边形.
(1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
(3)现有图①中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
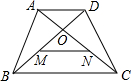 如图,ABCD是等腰梯形,对角线AC与BD交于O点,AD=2,M、N分别是OB、OC的中点,AN与DM互相平分,则BC等于
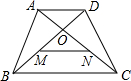
如图,ABCD是等腰梯形,对角线AC与BD交于O点,AD=2,M、N分别是OB、OC的中点,AN与DM互相平分,则BC等于查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com