
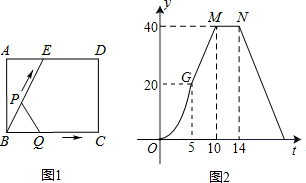
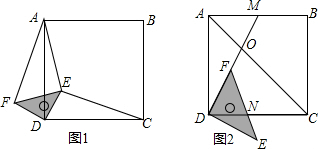
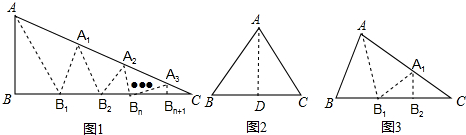
 如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①AD=BE=5;②当0<t≤5时,y=$\frac{4}{5}$t2;③cos∠ABE=$\frac{3}{5}$;④当t=$\frac{29}{2}$秒时,△ABE∽△QBP;⑤当△BPQ的面积为4cm2时,时间t的值是$\sqrt{10}$或$\frac{51}{5}$; 其中正确的结论是②④.
如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①AD=BE=5;②当0<t≤5时,y=$\frac{4}{5}$t2;③cos∠ABE=$\frac{3}{5}$;④当t=$\frac{29}{2}$秒时,△ABE∽△QBP;⑤当△BPQ的面积为4cm2时,时间t的值是$\sqrt{10}$或$\frac{51}{5}$; 其中正确的结论是②④. 分析 根据图(2)可以判断三角形的面积变化分为四段,①当点P在BE上运动,点Q到达点C时;②当点P到达点E时,点Q静止于点C,从而得到BC、BE的长度;③点P到达点D时,点Q静止于点C;④当点P在线段CD上,点Q仍然静止于点C时.
解答 解:根据图(2)可得,
当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度分别是1cm/秒、2cm/秒
∴BC=BE=10,
∴AD=BC=10.
∴①错误;
又∵从M到N的变化是4,
∴ED=4,
∴AE=AD-ED=10-4=6.
∵AD∥BC,
∴∠EBQ=∠AEB,
∴cos∠EBQ=cos∠AEB=$\frac{AE}{BE}=\frac{3}{5}$,
故③错误;
如图1,过点P作PF⊥BC于点F,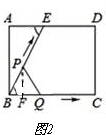
∵AD∥BC,
∴∠EBQ=∠AEB,
∴sin∠EBQ=sin∠AEB=$\frac{AB}{BE}$=$\frac{4}{5}$,
∴PF=PBsin∠EBQ=$\frac{4}{5}$t,
∴当0<t≤5时,y=$\frac{1}{2}$BQ×PF=$\frac{1}{2}$×2t×$\frac{4}{5}$t=$\frac{4}{5}$t2,
故②正确,
如图4,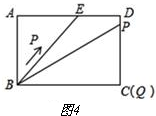
当t=$\frac{29}{2}$时,点P在CD上,
∴PD=$\frac{29}{2}$-BE-ED=$\frac{29}{2}$-10-4=$\frac{1}{2}$,
PQ=CD-PD=8-$\frac{1}{2}$=$\frac{15}{2}$,
∴$\frac{AB}{AE}=\frac{4}{3}$,$\frac{BQ}{PQ}=\frac{4}{3}$,
∴$\frac{AB}{AE}=\frac{BQ}{PO}$
∵∠A=∠Q=90°,
∴△ABE∽△QBP,
故④正确.
由②知,y=$\frac{4}{5}$t2
当y=4时,$\frac{4}{5}$t2=4,
从而$t=\sqrt{5}$,
故⑤错误
综上所述,正确的结论是②④.
点评 此题是二次函数综合题,主要考查了锐角三角函数,全等三角形的性质和判定,相似三角形的性质和判定,解本题的关键是线段的计算,也是本题的难点.


科目:初中数学 来源: 题型:解答题
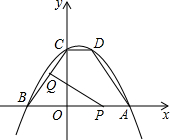 如图,抛物线y=ax2+bx+c经过点A(5,0),B(-3,0),C(0,4),过C作CD∥x轴交抛物线于D,连结BC、AD两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动,其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动,设这个两个动点运动的时间为t(秒)(0<t<7),△PQB的面积记为S.
如图,抛物线y=ax2+bx+c经过点A(5,0),B(-3,0),C(0,4),过C作CD∥x轴交抛物线于D,连结BC、AD两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动,其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动,设这个两个动点运动的时间为t(秒)(0<t<7),△PQB的面积记为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
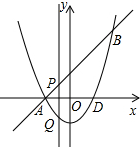 如图,抛物线与直线相交于A,B两点,若点A在x轴上,点B的坐标是(2,4),抛物线与x轴另一交点为D,并且△ABD的面积为6,直线AB与y轴的交点的坐标为(0,2).点P是线段AB(不与A,B重合)上的一个动点,过点P作x轴的垂线,交抛物线与点Q.
如图,抛物线与直线相交于A,B两点,若点A在x轴上,点B的坐标是(2,4),抛物线与x轴另一交点为D,并且△ABD的面积为6,直线AB与y轴的交点的坐标为(0,2).点P是线段AB(不与A,B重合)上的一个动点,过点P作x轴的垂线,交抛物线与点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
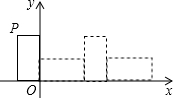 如图,把小矩形放在第二象限,使两条边与坐标轴重合,然后将小矩形无滑动的沿x轴顺时针滚动,每一次边落在x轴上记作一次操作,己知顶点P(-1,2),则经过2015次操作后点P的坐标为(3021,0).
如图,把小矩形放在第二象限,使两条边与坐标轴重合,然后将小矩形无滑动的沿x轴顺时针滚动,每一次边落在x轴上记作一次操作,己知顶点P(-1,2),则经过2015次操作后点P的坐标为(3021,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com