
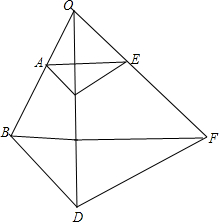
 如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是位似三角形吗?为什么?
如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是位似三角形吗?为什么? 分析 利用相似三角形的判定与性质得出△OAE∽△OBF,进而得出AE∥BF,再利用位似图形的定义求出即可.
解答  解:△ACE与△BDF是位似三角形,
解:△ACE与△BDF是位似三角形,
理由:∵AC∥BD,CE∥DF,
∴$\frac{OA}{OB}$=$\frac{OC}{OD}$,$\frac{OE}{OF}$=$\frac{OC}{OD}$,
∴$\frac{OA}{OB}$=$\frac{OE}{OF}$,
又∵∠AOE=∠BOF,
∴△OAE∽△OBF,
∴∠OAE=∠OBF,
∴AE∥BF,
又∵△ACE与△BDF对应点相交于点O,
∴△ACE与△BDF是位似三角形.
点评 此题主要考查了位似变换以及相似三角形的判定与性质,正确利用位似图形的定义得出是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$h≤z$<\frac{1}{3}$h | B. | $\frac{1}{3}$h≤z$<\frac{1}{2}$h | C. | $\frac{1}{2}$h≤z$<\frac{3}{4}$h | D. | $\frac{3}{4}h≤z<h$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{3y}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{3y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 玩具小狗件数(单位:个) | 玩具小汽车个数(单位:个) | 总时间(单位:分) | 总工资(单位:元) |
| 1 | 1 | 35 | 2.15 |
| 2 | 2 | 70 | 4.30 |
| 3 | 2 | 85 | 5.05 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com