
【题目】已知等边△ABC.
(1)如图①,P为等边△ABC外一点,且∠BPC=120°,试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想;
(2)如图②,P为等边△ABC内一点,且∠APD=120°,求证:PA+PD+PC>BD;
(3)在(2)的条件下,若∠CPD=30°,AP=4,CP=5,DP=8,求BD的长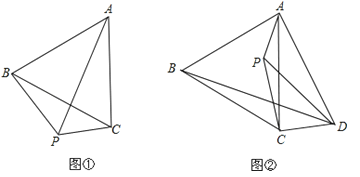
【答案】解:(1)AP=BP+PC,
证明:延长BP至E,使PE=PC,连接CE,如图1所示,
∵∠BPC=120°,
∴∠CPE=60°,
又∵PE=PC,
∴△CPE为等边三角形,
∴CP=PE=CE,∠PCE=60°,
∵△ABC为等边三角形,
∴AC=BC,∠BCA=60°,
∴∠ACB=∠PCE,
∴∠ACB+∠BCP=∠PCE+∠BCP,
即∠ACP=∠BCE,
在△ACP与△BCE中, ,
,
∴△ACP≌△BCE(SAS),
∴AP=BE,
∵BE=BP+PE,
∴AP=BP+PC;
(2)证明:延长DP到M使得PM=PA,连接AM、BM,如下图2所示,
∵∠APD=120°,PM=PA,
∴∠APM=60°,
∴△APM是等边三角形,
∴AM=AP,∠PAM=60°,
∴DM=PD+PA,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠MAP=∠BAC,
∴∠MAP﹣∠BAP=∠BAC﹣∠BAP,
即∠MAB=∠PAC,
在△AMB和△APC中,
∴△AMB≌△APC(SAS)
∴BM=PC,
∵在△BDM中,DM+BM>BD,DM=PD+PA,
∴PA+PD+PC>BD.
(3)如下图2所示,
由(2)知△AMB≌△APC,
∴MB=PC,∠AMB=∠APC,
∵∠CPD=30°,AP=4,CP=5,DP=8,∠APD=120°,∠AMP=60°,
∴MB=5,∠AMB=∠APC=∠APD+∠CPD=120°+30°=150°,
∴∠BMD=∠AMB﹣∠AMP=90°,
∵MD=MP+PD=4+8=12,MB=5,
∴BD=![]() =13,
=13,
故答案为:13.
【解析】(1)先写出线段BP、PC、AP之间的数量关系,然后根据猜想作出合适的辅助线,画出相应的图形,找出所求数量关系需要的条件即可;
(2)要证明PA+PD+PC>BD,只需要作辅助线延长DP到M使得PM=PA,连接AM、BM,画出相应的图形,根据三角形两边之和大于第三边即可证明结论;
(3)要求BD的长,根据(2)中得到的结论和题意可以得到∠BMD=90°,BM的长,MD的长,然后根据勾股定理即可求得BD的长,本题得以解决.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22016的值,可设S=1+2+22+23+…+22016 , 于是2S=2+22+23+…+22017 , 因此2S﹣S=22017﹣1,所以S=22017﹣1.我们把这种求和方法叫错位相减法.仿照上述的思路方法,计算出1+5+52+53+…+52016的值为( )
A.52017﹣1
B.52016﹣1
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
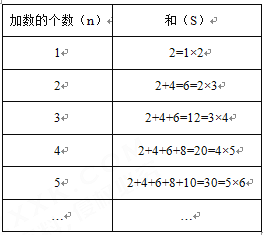
【题目】从2开始,连续的偶数相加,它的和的情况如下表:
(1)当n个最小的连续偶数相加时,它们的和s与n之间的关系式为s= (用含n的式子表示)
(2)并由此计算:
①2+4+6+8+…+50;
②52+54+56+…+100.
查看答案和解析>>
科目:初中数学 来源: 题型:
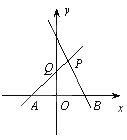
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某朋的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22),若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为( )
A.32
B.126
C.135
D.144
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com