
ЁОЬтФПЁПШчЭМЃЌдкЖЋЮїЗНЯђЕФКЃУцЯп![]() ЩЯЃЌга
ЩЯЃЌга![]() ЃЌ
ЃЌ![]() СНЫвбВТпДЌКЭЙлВтЕу
СНЫвбВТпДЌКЭЙлВтЕу![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дкжБЯп
дкжБЯп![]() ЩЯЃЉЃЌСНДЌЭЌЪБЪеЕНгцДЌ
ЩЯЃЉЃЌСНДЌЭЌЪБЪеЕНгцДЌ![]() дкКЃУцЭЃжЭЕуЗЂГіЕФЧѓОШаХКХЃЎВтЕУгцДЌЗжБ№дкбВТпДЌ
дкКЃУцЭЃжЭЕуЗЂГіЕФЧѓОШаХКХЃЎВтЕУгцДЌЗжБ№дкбВТпДЌ![]() ЃЌ
ЃЌ![]() ББЦЋЮї
ББЦЋЮї![]() КЭББЦЋЖЋ
КЭББЦЋЖЋ![]() ЗНЯђЃЌбВТпДЌ
ЗНЯђЃЌбВТпДЌ![]() КЭгцДЌ
КЭгцДЌ![]() ЯрОр120КЃРяЃЌгцДЌдкЙлВтЕу
ЯрОр120КЃРяЃЌгцДЌдкЙлВтЕу![]() ББЦЋЖЋ
ББЦЋЖЋ![]() ЗНЯђЃЎЃЈЫЕУїЃКНсЙћШЁећЪ§ЃЎВЮПМЪ§ОнЃК
ЗНЯђЃЎЃЈЫЕУїЃКНсЙћШЁећЪ§ЃЎВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЎЃЉ
ЃЎЃЉ
ЃЈ1ЃЉЧѓбВТпДЌ![]() гыЙлВтЕу
гыЙлВтЕу![]() МфЕФОрРыЃЛ
МфЕФОрРыЃЛ
ЃЈ2ЃЉвбжЊЙлВтЕу![]() ДІ45КЃРяЕФЗЖЮЇФкгаАЕНИЃЎШєбВТпДЌ
ДІ45КЃРяЕФЗЖЮЇФкгаАЕНИЃЎШєбВТпДЌ![]() би
би![]() ЗНЯђШЅгЊОШгцДЌ
ЗНЯђШЅгЊОШгцДЌ![]() гаУЛгаДЅНИЕФЮЃЯеЃПВЂЫЕУїРэгЩЃЎ
гаУЛгаДЅНИЕФЮЃЯеЃПВЂЫЕУїРэгЩЃЎ
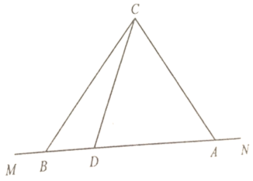
ЁОД№АИЁПЃЈ1ЃЉ76КЃРяЃЛЃЈ2ЃЉУЛгаДЅНИЕФЮЃЯеЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉзї![]() ЃЎИљОнжБНЧШ§НЧаЮаджЪЧѓAEЃЌCE,ABЃЌдйжЄ
ЃЎИљОнжБНЧШ§НЧаЮаджЪЧѓAEЃЌCE,ABЃЌдйжЄ![]() ЃЎЫљвд
ЃЎЫљвд![]() ЃЎ
ЃЎ
ЃЈ2ЃЉзї![]() ЃЎжЄBF=DFЃЌгЩBF2+DF2=BD2ПЩЧѓНт.
ЃЎжЄBF=DFЃЌгЩBF2+DF2=BD2ПЩЧѓНт.
НтЃКЃЈ1ЃЉзї![]() ЃЎ
ЃЎ
вђЮЊгцДЌЗжБ№дкбВТпДЌ![]() ЃЌ
ЃЌ![]() ББЦЋЮї
ББЦЋЮї![]() КЭББЦЋЖЋ
КЭББЦЋЖЋ![]() ЗНЯђЃЌ
ЗНЯђЃЌ
ЫљвдЁЯCAE=60Ёу, ЁЯCBE=45Ёу
ЫљвдЁЯACE=30Ёу, ЁЯACB=180Ёу-60Ёу-45Ёу=75Ёу;
Ыљвд![]() ЃЈКЃРяЃЉЃЌ
ЃЈКЃРяЃЉЃЌ![]() ЃЈКЃРяЃЉЃЎ
ЃЈКЃРяЃЉЃЎ

Ыљвд![]() ЃЎ
ЃЎ
вђЮЊгцДЌдкЙлВтЕу![]() ББЦЋЖЋ
ББЦЋЖЋ![]() ЗНЯђЃЎ
ЗНЯђЃЎ
ЫљвдЁЯCDE=75
ЫљвдЁЯCDE=ЁЯACB,
Ыљвд![]() ЃЎ
ЃЎ
Ыљвд![]() ЃЎ
ЃЎ
МД![]() ЃЎ
ЃЎ
НтЕУЃЌ![]() ЃЎ
ЃЎ
Ёр![]() КЃРяЃЎ
КЃРяЃЎ
ЃЈ2ЃЉУЛгаДЅНИЕФЮЃЯеЃЎ
зї![]() ЃЎ
ЃЎ
вђЮЊЁЯCBD=45Ёу
ЫљвдBF=DF
ЫљвдBF2+DF2=BD2
МДDF2+DF2=762
ПЩЧѓЕУ![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
ЁрУЛгаДЅНИЕФЮЃЯеЃЎ


 УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНx2+bxЉtЕФЖдГЦжсЮЊxЃН2ЃЎШєЙигкxЕФвЛдЊЖўДЮЗНГЬx2+bxЉtЃН0дкЉ1ЃМxЃМ3ЕФЗЖЮЇФкгаЪЕЪ§НтЃЌдђtЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A. Љ4ЁмtЃМ5B. Љ4ЁмtЃМЉ3C. tЁнЉ4D. Љ3ЃМtЃМ5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kxЃЋbгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓЯрНЛгкA(2ЃЌ4)ЁЂB(Ѓ4ЃЌn)СНЕуЃЎ
ЕФЭМЯѓЯрНЛгкA(2ЃЌ4)ЁЂB(Ѓ4ЃЌn)СНЕуЃЎ
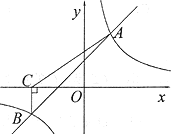
(1)ЗжБ№ЧѓГівЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
(2)ИљОнЫљИјЬѕМўЃЌЧыжБНгаДГіВЛЕШЪНkxЃЋbЃО![]() ЕФНтМЏ ЃЛ
ЕФНтМЏ ЃЛ
(3)Й§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊЕуCЃЌСЌНгACЃЌЧѓSЁїABCЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЯьгІЪаеўИЎКХейЃЌФГаЃПЊеЙСЫЁАСљГЧЭЌДДгыЮвЭЌааЁБЛюЖЏжмЃЌЛюЖЏжмЩшжУСЫЁАAЃКЮФУїРёвЧЃЌBЃКЩњЬЌЛЗОГЃЌCЃКНЛЭЈАВШЋЃЌDЃКЮРЩњБЃНрЁБЫФИіжїЬтЃЌУПИібЇЩњбЁвЛИіжїЬтВЮгыЃЎЮЊСЫНтЛюЖЏПЊеЙЧщПіЃЌбЇаЃЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌВЂИљОнЕїВщНсЙћЛцжЦСЫШчЯТЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЎ
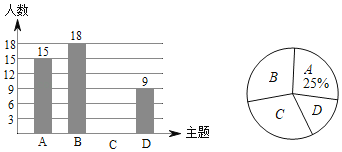
(1)БОДЮЫцЛњЕїВщЕФбЇЩњШЫЪ§ЪЧ______ШЫЃЛ
(2)ЧыФуВЙШЋЬѕаЮЭГМЦЭМЃЛ
(3)дкЩШаЮЭГМЦЭМжаЃЌЁАBЁБЫљдкЩШаЮЕФдВаФНЧЕШгк______ЖШЃЛ
(4)аЁУїКЭаЁЛЊИїздЫцЛњВЮМгЦфжаЕФвЛИіжїЬтЛюЖЏЃЌЧыгУЛЪїзДЭМЛђСаБэЕФЗНЪНЧѓЫћУЧЧЁКУбЁжаЭЌвЛИіжїЬтЛюЖЏЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
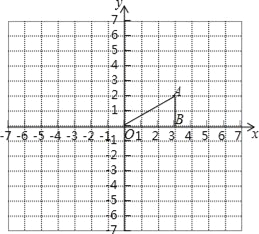
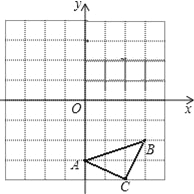
ЁОЬтФПЁПШчЭМЃЌЕуAЕФзјБъЮЊЃЈ3ЃЌ2ЃЉЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЎзїШчЯТВйзїЃК
ЃЈ1ЃЉвдЕуAЮЊа§зЊжааФЃЌНЋЁїABOЫГЪБеыЗНЯђа§зЊ90ЁуЃЌЕУЕНЁїAB1O1ЃЛ
ЃЈ2ЃЉвдЕуOЮЊЮЛЫЦжааФЃЌНЋЁїABOЗХДѓЃЌЕУЕНЁїA2B2OЃЌЪЙЮЛЫЦБШЮЊ1ЃК2ЃЌЧвЕуA2дкЕкШ§ЯѓЯоЃЎ
ЂйдкЭМжаЛГіЁїAB1O1КЭЁїA2B2OЃЛ
ЂкЧыжБНгаДГіЕуA2ЕФзјБъЃКЁЁЁЁЃЎ
ЂлШчЙћЁїABOФкВПвЛЕуMЕФзјБъЮЊЃЈmЃЌnЃЉЃЌаДГіЕуMдкЁїA2B2OФкЕФЖдгІЕуNЕФзјБъЃКЁЁЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЁїABCШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈ0ЃЌЉ3ЃЉЁЂBЃЈ3ЃЌЉ2ЃЉЁЂCЃЈ2ЃЌЉ4ЃЉЃЌе§ЗНаЮЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЪЧ1ИіЕЅЮЛГЄЖШЃЎ
ЃЈ1ЃЉЛГіЁїABCЯђЩЯЦНвЦ6ИіЕЅЮЛЕУЕНЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉвдЕуCЮЊЮЛЫЦжааФЃЌдкЭјИёжаЛГіЁїA2B2C2ЃЌЪЙЁїA2B2C2гыЁїABCЮЛЫЦЃЌЧвЁїA2B2C2гыЁїABCЕФЮЛЫЦБШЮЊ2ЃК1ЃЌВЂжБНгаДГіЕуA2ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊОиаЮ ABCD ЕФвЛЬѕБп AD=8ЃЌНЋОиаЮ ABCD елЕўЃЌЪЙЕУЖЅЕу B Тфдк CD БпЩЯЕФ P ЕуДІЃЎ
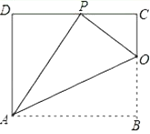
ЃЈ1ЃЉЧѓжЄЃКЁїOCPЁзЁїPDAЃЛ
ЃЈ2ЃЉШєЁїOCP гыЁїPDA ЕФУцЛ§БШЮЊ 1ЃК4ЃЌЧѓБп AB ЕФГЄЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
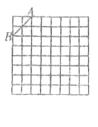
ЁОЬтФПЁПШчЭМЃЌЪЧЙцИёЮЊ8ЁС8ЕФе§ЗНаЮЭјИёЃЌЧыдкЫљИјЕФЭјИёжаАДЯТСавЊЧѓВйзї.
ЃЈ1ЃЉдкЭјИёжаНЈСЂЦНУцжБНЧзјБъЯЕЃЌЪЙЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() .
.
ЃЈ2ЃЉдкЕкЖўЯѓЯоФкЕФИёЕуЩЯЛвЛЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() гыЯпЖЮ
гыЯпЖЮ![]() зщГЩвЛИівд
зщГЩвЛИівд![]() ЮЊЕзЕФЕШбќШ§НЧаЮЃЌЧвбќГЄЪЧЮоРэЪ§.ЧѓЕу
ЮЊЕзЕФЕШбќШ§НЧаЮЃЌЧвбќГЄЪЧЮоРэЪ§.ЧѓЕу![]() ЕФзјБъМА
ЕФзјБъМА![]() ЕФжмГЄЃЈНсЙћБЃСєИљКХЃЉ.
ЕФжмГЄЃЈНсЙћБЃСєИљКХЃЉ.
ЃЈ3ЃЉНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ90ЁуКѓЕУЕН
ЫГЪБеыа§зЊ90ЁуКѓЕУЕН![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊЮЛЫЦжааФНЋ
ЮЊЮЛЫЦжааФНЋ![]() ЗХДѓЃЌЪЙЗХДѓЧАКѓЕФЮЛЫЦБШЮЊ1ЃК2ЃЌЛГіЗХДѓКѓЕФ
ЗХДѓЃЌЪЙЗХДѓЧАКѓЕФЮЛЫЦБШЮЊ1ЃК2ЃЌЛГіЗХДѓКѓЕФ![]() ЕФЭМаЮ.
ЕФЭМаЮ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯAЃН90ЁуЃЌЁЯADCЃН120ЁуЃЌСЌНгBDЃЌАбЁїABDбиBDЗелЃЌЕУЕНЁїAЁфBDЃЌСЌНгAЁфCЃЌШєABЃН3ЃЌЁЯABDЃН60ЁуЃЌдђЕуDЕНжБЯпAЁфCЕФОрРыЮЊЃЈЁЁЁЁЃЉ
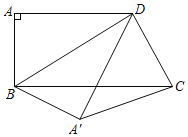
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com