
����Ŀ��Ϊ����ѧ������ѧ������ijѧУ��չ�ˡ���ѧ�����������.���꼶![]() ��ѧ���μ��˾������������ѧ���ɼ���������
��ѧ���μ��˾������������ѧ���ɼ���������![]() ��(����
��(����![]() ��)��Ϊ���˽�ɼ��ֲ������ѧУ�����ȡ�˲���ѧ���ijɼ�����ͳ�ƣ��õ����²�������ͳ�Ʊ������ݱ���������Ϣ������������⣺
��)��Ϊ���˽�ɼ��ֲ������ѧУ�����ȡ�˲���ѧ���ijɼ�����ͳ�ƣ��õ����²�������ͳ�Ʊ������ݱ���������Ϣ������������⣺
�ɼ� | Ƶ�� | Ƶ�� |
|
|
|
|
|
|
|
|
|
|
|
|
![]() ����
����![]() ___ _ _ ��
___ _ _ ��![]() _��
_��
![]() �������ݵ���λ������_____ _��Χ�ڣ�
�������ݵ���λ������_____ _��Χ�ڣ�
![]() ���ɼ���С��
���ɼ���С��![]() ��Ϊ���㣬����ƾ��꼶��Լ�ж�����ѧ���������ɼ���
��Ϊ���㣬����ƾ��꼶��Լ�ж�����ѧ���������ɼ���
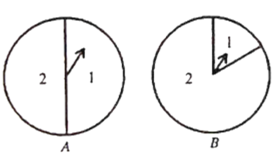
![]() ������������һ����Ŀ�� ��ͼ��������ת��
������������һ����Ŀ�� ��ͼ��������ת��![]() ��ÿ��ת�̸��Ե��������������зֱ��������1��2���ֱ�ת��ת��
��ÿ��ת�̸��Ե��������������зֱ��������1��2���ֱ�ת��ת��![]() ��ת��ֹͣת��ʱ�����¼���ָ�붼���ڱ�������
��ת��ֹͣת��ʱ�����¼���ָ�붼���ڱ�������![]() �����������ڡ�������
�����������ڡ�������![]() ����ת��
����ת��![]() �б�������
�б�������![]() �����ε�Բ�ĽǵĶ����� ��
�����ε�Բ�ĽǵĶ����� ��
���𰸡�![]()
![]() ��
��![]() ��
�� ![]() �����
��λ����![]() �ڣ�
�ڣ� ![]() ����
����![]()
��������
��1���ȸ���![]() �����������Ϊ50��ѧ�����ĸ�����������;���50���������
�����������Ϊ50��ѧ�����ĸ�����������;���50���������![]() ��ֵ��������֪
��ֵ��������֪![]() ��Ƶ�����������������
��Ƶ�����������������![]() ��
��
��2��������λ���ĸ��������𰸣�
��3�����������гɼ���С��![]() ��Ϊ�����Ƶ�ʼ��ɹ��������гɼ���С��
��Ϊ�����Ƶ�ʼ��ɹ��������гɼ���С��![]() �ֵ�ѧ��������
�ֵ�ѧ��������
��4���ȸ����������ת��B��ָ�����ڱ�������1�����������ڵĸ��ʣ��ٸ���Բ�ܽǵ���![]() ���㼴�ɣ�
���㼴�ɣ�
�⣺��1������ѧ��������![]() ��������
��������
![]() ��Ƶ����
��Ƶ����![]() ����
����![]() ��
��
![]() ��Ƶ�ʣ�
��Ƶ�ʣ�![]() ����
����![]() ��
��
�ʴ�Ϊ��20��0.2��
��2����50��ѧ������λ�����ڡ�![]() ����Χ�ڣ�
����Χ�ڣ�
��3������ѧ���У��ɼ���С��![]() �ֵ�Ƶ�ʣ�
�ֵ�Ƶ�ʣ�![]() ��
��
���Ը��������������壬���꼶�������ɼ���ѧ��������![]() ��������
��������
�����꼶��Լ��360��ѧ���������ɼ���
��4����ת��B��ָ�����ڱ�������1�����������ڵĸ���Ϊ![]() ��
��
��������ã�![]() ��
��
���![]() ��
��
����ת��B��ָ�����ڱ�������1�����ε�Բ�ĽǵĶ���Ϊ��![]() ��
��
�ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С�Ź���100ֻ�����ͺŵ��ľ߽������ۣ�����ۺ��ۼ�֮��Ĺ�ϵ���±���
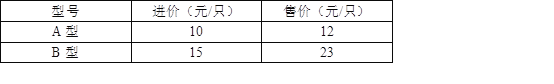
��1��С����ν�����ʹ������ǡ��Ϊ1300Ԫ��
��2��Ҫʹ�����ľ�����������������������������۸��40%�������С�����һ�������������������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
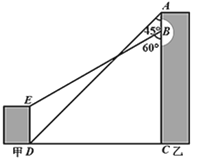
����Ŀ����ͼ��ij���мס������������С������¥¥��A�㴦����¥¥��D�㴦�ĸ���Ϊ45�㣬�ߵ���¥B�㴦����¥¥��E�㴦�ĸ���Ϊ60�㣬��֪AB=6m��DE=10m.����¥�ĸ߶�AC�ij�.���ο����ݣ�![]() ��
��![]() ����ȷ��0.1m.��
����ȷ��0.1m.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ACB�У���ACB=90����AC=2BC=4����PΪAB���е㣬��EΪAC���ϲ���˵��غϵ�һ���㣬����ADP����ֱ��PD�۵�����PDE����DE��AB����AD�ij���Ϊ_____ ��
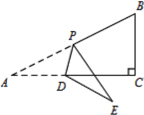
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�����ڼ�Ϊ����ʵץ����ͣ�β�ͣѧ���������ij����ƽ̨�����ȡ�˸�У����ѧ��������ѧϰʱ�䣬����������Ƴ�����������������ͳ��ͼ��

�������������Ϣ�ش���������
��1�����ε��������Ϊ������ ѧϰʱ��Ϊ7Сʱ�����Ե�Բ�Ľ�Ϊ ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����ȫУ����ѧ��1800�ˣ������ж���ѧ������ѧϰʱ�䲻����8��Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c������(��1��0)����y�ύ��(0��2)�������ߵĶԳ���Ϊֱ��x��1�������н����У���a+c��b���ڷ���ax2+bx+c��0�Ľ�Ϊ��1��3����2a+b��0����c��a��2��������ȷ�Ľ����У� ��
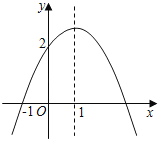
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������B(1��0)��������![]() ��y�ύ�ڵ�C���䶥��Ϊ��G������C��y��Ĵ��߽������߶Գ����ڵ�D���߶�CO����һ����M������DM��DG��
��y�ύ�ڵ�C���䶥��Ϊ��G������C��y��Ĵ��߽������߶Գ����ڵ�D���߶�CO����һ����M������DM��DG��
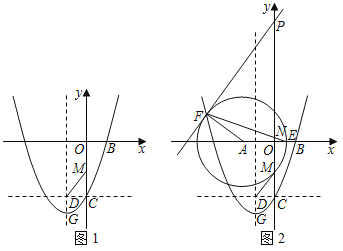
��1���������ߵı���ʽ��
��2����![]() ����Сֵ�Լ���Ӧ�ĵ�M�����ꣻ
����Сֵ�Լ���Ӧ�ĵ�M�����ꣻ
��3����ͼ2���ڣ�2���������£��Ե�A(��2��0)ΪԲ�ģ���AM��Ϊ�뾶��Բ��x���������ڵ�E����y������������һ����P��ֱ��PF���A�����ڵ�F������EF��y���ڵ�N����PF��BMʱ����PN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��4��CΪ����BA��һ���㣬��BCΪ����������������BCD����O��A��C��D���㣬EΪ��O��һ�㣬����AD��ED��ֱ��CE��ֱ��AD��F��
��1����֤��CE��BD��
��2����CF=a����C���߶�AB���˶���
�����E�˶���·������
����a�ķ�Χ��
��3����AC��1���� tan��DEC��
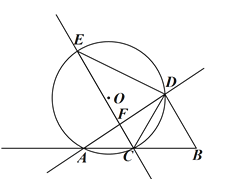
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ٴ�·�ţ���ͼ�٣����Ϸ���ĸ�ө����Ǻӣ���λ�ںϷ��ж�����ͨ���ɵ��ٴ�·�ϣ�������1987����ף�Ϊ�г�ʽ�ֽ��ţ�tong�����ţ��ŵ��ϲ��ṹΪ2���ֽ�����������ι��ߣ���ͼ�����Ź��ߵļ�ʾ��ͼ�����й�������AB��Լ100�ף�
��1����ͼ���У������ó߹���ͼ�ķ��������ҳ���AB����Բ��Բ��O��Ȼ��ȷ����AB����AB���е�C��D������Ҫд��������������ͼ�ۼ���
��2����ͼ���У�����AOB��80������ù��Ÿ�CDԼΪ�����ף��������ȷ��0.1�ף��ο����ݣ�sin50���0.77��cos50���0.6��tan50���1.19��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com