
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 因为a,b,c满足|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2=2+2ac,则这个等式必须有意义,则 $\sqrt{(a-3){b}^{2}}$必有意义,从而确定a的取值,然后将a的值代入等式
|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2-2ac=2,分析等式的特征并确定b、c的值即可
解答 解:∵已知a,b,c满足|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2=2+2ac,
∴|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2-2ac=2,…①
且$\sqrt{(a-3){b}^{2}}$必有意义,
又∵b2≥0,
∴a-3≥0
①当a-3>0时,|2a-4|>2,
有|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2-2ac>2,
则这与①式相矛盾,即a-3>0不成立;
②当a-3=0时,a=3,则
|2a-4|+|b+2|+$\sqrt{(a-3){b}^{2}}$+a2+c2-2ac=2+|b+2|+0+(c-3)2=2,
|b+2|+(c-3)2=0,
又∵|b+2|≥0,(c-3)2≥0,
∴必有b+2=0,c-3=0
即:b=-2,c=3
∴a-b+c=3-(-2)+3=8
故:选D
点评 本题考查了二次根式有意义的条件、配方法的应用、几个非负数的和为零的条件等知识点;解题的关键是根据条件中等式的特点及二次根式有意义的条件确定a、b、的取值c


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 25 | 29 | 32 | 34 | 35 | 38 | 40 |
| 人数(人) | 2 | 4 | 3 | 7 | 9 | 7 | 6 |
| A. | 该班一共有38名同学 | |
| B. | 该班学生这次考试成绩的众数是35分 | |
| C. | 该班学生这次考试成绩的中位数是35分 | |
| D. | 该班学生这次考试成绩的平均数是35分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
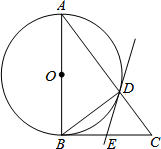 如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形网格(每个小正方形边长为1)中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做个点三角形.
如图,正方形网格(每个小正方形边长为1)中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做个点三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com