
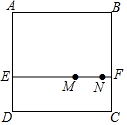
 如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN=$\frac{1}{3}$EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是3$\sqrt{3}$cm.
如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN=$\frac{1}{3}$EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是3$\sqrt{3}$cm. 分析 当正方形纸片卷成一个圆柱,点A与点B重合时,EF卷成一个圆,MN卷成圆上一段弧,该段弧所对的圆心角为$\frac{1}{3}$×360°,要求圆柱上M,N两点间的距离即求弦MN的长.
解答 解:根据题意得:EF=AB=DC,MN=$\frac{1}{3}$EF,
把该正方形纸片卷成一个圆柱,使点A与点B重合,则线段EF形成一直径为6cm的圆,MN为圆上的一段弧.
$\widehat{MN}$所对的圆心角为:$\frac{1}{3}$×360°=120°,
120°÷2=60°,
所以圆柱上M,N两点间的距离为:2×(6÷2)×sin60°=3$\sqrt{3}$cm.
故答案为:3$\sqrt{3}$.
点评 此题实质考查了圆上弦的计算,需要先找出圆心角再根据弦长公式计算,熟练掌握公式及性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )
小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )| A. | 同时抛掷两枚硬币,落地后两枚硬币正面都朝上 | |
| B. | 一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃 | |
| C. | 抛一个质地均匀的正方体骰子,朝上的面点数是3 | |
| D. | 一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
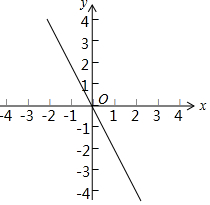 已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图象交于A、B两点(点A在点B的右侧),与其对称轴交于点C.
已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图象交于A、B两点(点A在点B的右侧),与其对称轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
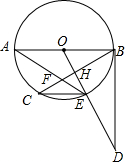 如图,AB是⊙O的直径,BC是弦,过点O作OE⊥BC于H交⊙O于E,在OE的延长线上取一点D,使∠ODB=∠AEC,AE与BC交于F.
如图,AB是⊙O的直径,BC是弦,过点O作OE⊥BC于H交⊙O于E,在OE的延长线上取一点D,使∠ODB=∠AEC,AE与BC交于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com