
分析 (1)求出1,2,3三个数中偶数的个数,再直接根据概率公式求解即可;
(2)分别列举出可能组成的两位数,再根据概率公式解答即可.
解答 解:(1)随机地抽取一张,所有可能出现的结果有3个,每个结果发生的可能性都相等,其中卡片上的数字为偶数的结果有1个.
故从袋中任意抽取一张卡片,则抽出的是偶数的概率为:$\frac{1}{3}$;
故答案为:$\frac{1}{3}$;
(2)解法一:列举法
被抽取的两张卡片所有可能是:1、2;1、3;2、3.
而每一种情况,都可构成两个两位数,
即是:12,21,13,31,23,32,
共6个两位数.其中是奇数的为:
21,13,31,23共4个,
∴P(奇数)=$\frac{4}{6}$=$\frac{2}{3}$.
解法二:列表法
| 1 | 2 | 3 | |
| 1 | 12 | 13 | |
| 2 | 21 | 23 | |
| 3 | 31 | 32 |

点评 此题主要考查了列举法求概率,用到的知识点为:概率=所求情况数与总情况数之比.得到所求的情况数是解决本题的易错点.


科目:初中数学 来源: 题型:选择题
| A. | x$≤-\frac{1}{2}$ | B. | x$≥-\frac{1}{2}$ | C. | x$<-\frac{1}{2}$ | D. | x$>-\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
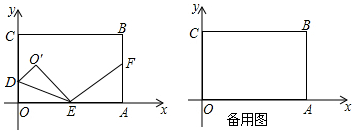
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com